《反相吧刊》
创刊号
第1卷第1期 (Vol.1 No.1)
2010.04.15.
四维时空间隔的几何诠释
在相对论中,定义四维标量
![]() (1)
(1)
 为两事件间隔,并由此推断出空间和时间是密不可分的‘时—空’统一体。对于这一推断正确是否暂不评论,我们先来讨论(1)式是如何导出的。
为两事件间隔,并由此推断出空间和时间是密不可分的‘时—空’统一体。对于这一推断正确是否暂不评论,我们先来讨论(1)式是如何导出的。
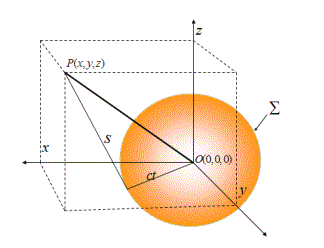
图1 四维时空间隔的几何关系
从图1易看出,若在
![]() 时刻,静止于三维直角坐标系
时刻,静止于三维直角坐标系
![]() 原点
原点
![]() 处的光源开始辐射球面波
处的光源开始辐射球面波
![]() ,相对于
,相对于
![]() 点观测者而言,在
点观测者而言,在
![]() 时刻,波前
时刻,波前
![]() 的波振面方程是同(1)式四维时空间隔的形式完全一致。据此(1)式应理解为是静止光源辐射电磁波的波振面方程,
的波振面方程是同(1)式四维时空间隔的形式完全一致。据此(1)式应理解为是静止光源辐射电磁波的波振面方程,
![]() 是
是
![]() 时刻
时刻
![]() 点到波振面的切线长度,
点到波振面的切线长度,
![]() 情形是波前在
情形是波前在
![]() 时刻还尚未到达
时刻还尚未到达
![]() 点;
点;
![]() 情形是波前在
情形是波前在
![]() 时刻恰好到达
时刻恰好到达
![]() 点,此时的波振面方程为
点,此时的波振面方程为
![]() (2)
(2)
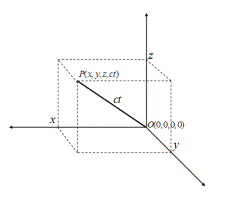 波振面上任意一点的坐标是可以用四维坐标
波振面上任意一点的坐标是可以用四维坐标
![]() 或
或
![]() 来描述,并可以在三维直角坐标系中把这一点表示出来,见图2所示。四维坐标点在三维坐标中实际上就是一个具有长度为ct的矢量。
来描述,并可以在三维直角坐标系中把这一点表示出来,见图2所示。四维坐标点在三维坐标中实际上就是一个具有长度为ct的矢量。
图2 四维坐标点的几何描述
如果球面波不是静止于
![]() 点的光源辐射,而是在
点的光源辐射,而是在
![]() 时刻以速度
时刻以速度
![]() 运动的光源在通过
运动的光源在通过
![]() 点瞬间辐射的球面波,在
点瞬间辐射的球面波,在
![]() 时刻,这个球面波上的任意点
时刻,这个球面波上的任意点
![]() 则一定满足波振面方程
则一定满足波振面方程
![]() (3)
(3)
须要指出,上面带撇坐标仅表明是运动光源辐射球面波的方程,不能认为它是相对于动系的坐标,这里没有动系,只有一个静系和光源相对这个静系静止和运动两种情形。
由麦克斯韦电磁理论知道,满足(2)式的电磁波波函数是
![]() (4)
(4)
其中,
![]() ;
;
![]() 是波矢方向上的单位矢量;
是波矢方向上的单位矢量;
![]() ;
;
![]() 是静止光源辐射的球面波其波前沿
是静止光源辐射的球面波其波前沿
![]() 方向相对静系的传播速度。满足(3)式的电磁波波函数是
方向相对静系的传播速度。满足(3)式的电磁波波函数是
![]() (5)
(5)
其中
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() 是运动光源辐射的球面波其波前沿
是运动光源辐射的球面波其波前沿
![]() 方向相对静系的传播速度。
方向相对静系的传播速度。
如果假设
![]() 和
和
![]() 含有的电磁波波数相同,则必有
含有的电磁波波数相同,则必有
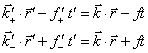 (6)
(6)
也就是有
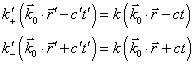 (7)
(7)
上面两式两边分别相乘,则有
![]() (8)
(8)
显然,若令
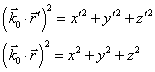 (9)
(9)
及
![]() (10)
(10)
就可得到
![]() (11)
(11)
可见,(11)式的导出并非是通过假设
![]() 后,由(1)式导出的,而是通过假设
后,由(1)式导出的,而是通过假设
![]() 和
和
![]() 含有的电磁波波数相同,由(6)式导出。满足(11)式的变换式,一定是满足电磁波相位不变变换式。与‘时—空’变换毫无关系,也根本不存在‘时—空’变换式及‘时—空’不变间隔。
含有的电磁波波数相同,由(6)式导出。满足(11)式的变换式,一定是满足电磁波相位不变变换式。与‘时—空’变换毫无关系,也根本不存在‘时—空’变换式及‘时—空’不变间隔。