返回首页
联络我们
易迪福网站地图
易迪科普知识
海外中文网导航
易迪 导航首页
易迪网站地图
海内外中文网站总导航
狭义相对性原理 :
所有的惯性参考系中,物理规律是一样的。广义相对性原理 :
所有的参考系中,物理规律是一样的。
爱因斯坦说 :" 所谓空间和时间都不过是人脑中一种执着的幻像而已。 "
爱因斯坦方程:
G-ab=T-ab
的思想精髓:物质等于时空的弯曲。
熵 S是能量 U与温度 T的商。
S=U/T
" 在这个社会里,有些事情不会发生,原因在于尺度。人类的尺度以米为单位 , 而宇宙的尺度以光年为单位 ."-- 张轩中
《沁 园春相对论》
张轩中
流形风光 , 千里度量 ,
万里联络。望黑洞内外 ,空间莽莽;宇宙上下,时光滔滔。霍金辐射,黑暗能量,爱翁上帝试比高。须他日,看彭罗斯图,分外妖娆。天才如此稀少,引无数凡夫竞折腰。惜英伦莎玛,仅搞教学;美国惠勒,年事已高。一代天骄,贝肯斯坦,只识黑洞用熵搞。
俱往矣,数风流人物,还看今朝。
科学的历史告诉我们:非常接近真理和真正懂得它的意义是两回事。每一个重要的理论都被它的发现者之前的人说过。
广义相对论
快子 物理网上教学
(1)
如何写论文
Relativity
sciencemag nasa.gov
Wikipedia
Blog
for Curious General
relativity special
relativity
Anti-
testing
general relativity NASA(Q&A)
SP(Q&A)
GR(search)
Astrophysicist
NASA NASA(cn)
引力探测器B
相对论 ( 上 )
( 下 )
吧主协议
贴吧介绍
贴吧帮助吧 jiusheng
qinqi e-huaxia
A-GG SP
易迪言论
网易博客
incinc
写作软件比较表
投稿
民科 (
永动机
吧根号√ √3,根号内很长时要加括号 √(3x+7)
相对论 (Relativity)研究物体的高速运动效应以及相关的动力学规律
爱因斯坦如是说:
1、物理体系的状态据以变化的定律,同描述这些状态变化时所参照的坐标系究竟是两个在互相匀速移动着的坐标系中的哪一个并无关系(相对性原理)。
2、任何光线在静止的坐标系中都是以确定的速度 c运动着,不管这道光线是由静止的还是运动的物体发射出来的(光速不变原理)。
简单说说与相对论有关的几个最根本问题。
因此,将“光速”作为观测工具,也就意味着,以相对论进行物理描述和研究时,是绝对不会出现“超光速”的观测事件。请注意,是观测事件,它不仅是指单个物体的相对运动,也包括多个物体的相对运动。。。。如果这样表述可能更容易理解:在任意观测事件中,不同参考系之间的相对速度恒小于光速。于是我说
“
火并 ”“ 王伦 ” 会有期 --
给相对论吧主的一封公开贴
开宗明义,本人基本立场是相信相对论理论的,但也认为相对论不是 “ 万能 ” 的。作为一个 “ 维相 ” 人士,来反相吧有几天了,感觉还不错。
刚来时就看到了反相吧吧主的 “ 本人反相基本观点 ” 一贴,先不说学术上的对错与否,感到的就是做人的大气,立场观点明确。同时,也发现这里比较活跃,所谓 “ 反相派 ” , “ 修相派 ” , “ 维相派 ” 都能畅所欲言。至于是否有那种莫名其妙删贴现象,由于来的时间短,暂时我还不清楚。总之,我认为办吧就要办成一个这样比较活跃而又有学术自由的吧。
离开相对论吧也有几天了,也有一些感叹。如果要形象地说明相对论吧的管理现状,只能说使我想起了 <<水浒 >>中王伦式的人物。作为吧主,学术水平倒是次要的,关键是要有学术上的科学自由思想,要有学术上的开放胸襟,要有公正的管理水平。相对论吧某吧主自己想想:在整个百度贴吧中,是否还能找出第二个象你一样使许多人如此反感的吧主!
随便举个例子,拿某网友 “ 土星 “ 人 ” 测定的光速是多少呢? ” 这个贴子来说,作为了解相对论的人士是应该能自信而又能很好说明这个问题的。但相吧吧主不但不正面回答问题,还以 “ 本贴标提前未加 “ 个人观点 ” ,不着边际的回复均已删除。 ” 作为理由来删除。试想,如果相吧吧主能正面回答的话,别人又怎么会 “ 不着边际的回复 ” 呢?试想,如果相吧吧主回答不了,又怎么不请包括相吧某 “ 姑奶奶 ” 式的人物来回答呢?其实就是 “ 翻版王伦 ” 而已!
又如,相吧吧主自己的那个 “ [狭义相对论常见问题解释 ]
关于同时的相对性 ” 的贴子,看看一大堆跟贴就知道相吧吧主没有把 “ 问题解释 ” 解释清楚,有人质疑相吧吧主在贴子中的某些内容是 “ 个人观点 ” 呢,还是抄袭来的,不但不正面回答,还莫名其妙地删掉了,这怎么能使人正常地讨论呢?其实,这个贴子在最起码的逻辑上就犯了一个不可原谅的错误,逻辑思维上常说,提出问题,分析问题,解决问题这样一个次序,而相吧吧主连 “ 同时的相对性 ” 的定义都不先明确提出,就试图解决问题,这无疑造成后来更多的混乱。更可笑的是自己把自己这有逻辑毛病的贴子加精,难道不怕有 “ 王婆卖瓜,自买自夸 ” 的嫌疑!
正因为如此,也因为这些事实,我本人走向了一条只 “ 反 ”“ 贪官 ” (现任某相对论吧主 ),不 “ 反 ”“ 皇帝 ” (相对论 )的道路,也期望大家能把反相对论吧发扬光大,办成一个讨论一切有关相对论的学术吧。这一定会是很有意义的事情!就现任某相对论吧主的行为来看,也祝相对论吧办成一个中学生或青少年学习相对论的一块 “ 学习 ” 园地!可叹的是那些在相对论吧中的真正高手也只好委屈去做个 “ 中学教师 ” 了!
最后,以一首打油诗来调侃一下相吧吧主:
删贴不要紧,只要有道理;删了这一个,还有下一个。
在网上,持不同意见者被 “ 拍砖头 ” 、群起而攻之的事并不少见,总会有一些网民喜欢扮演网络
“ 统治者 ” 的角色,只要是不符合自己观点的都是错的,都要号召网友一起将其赶尽杀绝。
对于持异见者,我们可以批判他的观点,但不应该封杀他,更不应该对其进行人身攻击。一个健康的社会,应该让每一个社会成员所持有的不同观点都能够表达出来,并尽可能地得到社会的倾听,即使 “ 我不同意你的观点,但我誓死捍卫你说话的权利 ” 。
人们常常讨论光速相对速度的问题,许多维相人士不敢正面回答或答非所问,那么,关于光速相对速度的问题,我试试回答如下:
理论上,第三者观测速度 =两物体的运动之和。
相对论只谈二者相互观察的关系,从二者相互观察的角度上才有它们之间的观察光速不大于光速,这是二者之间的一种连续而没有被打断的光。在某种意义上,也可以说是二者之间的一种变换关系,而 “ 第三者观测 ” 不涉及这种关系。
用二个相差比较近的速度作假设,如果 A相对于 C以 0.6c的速度向东运动, B相对于 C以 0.6c的速度向西运动。对于第三者 C来说, A和 B之间的距离以 1.2c的速度增大。这种 “ 速度 ” --两个运动物体之间相对于第三观察者的速度 --可以超过光速 (如果真有可能观察得到的话 )。但是两个物体分别与 C的速度没有超过光速 (0.6c)。两个物体相对于彼此的运动速度也没有超过光速。在这个例子中,根据相对论的观点和计算光速,在 A的坐标系中 B的速度是 0.88c。在 B的坐标系中 A的速度也是 0.88c。虽然 C看来 A和 B之间的距离以 1.2c的速度增大,但相对论者并不认为这是超光速,因为不是一束光,这也就是相对论的观点。
二个惯性系之间会有时空效应,二个惯性系的存在是绝对的,二个惯性系之间的运动速度(V)彼此看来是相对的,与此相连的时空效应也因而是相对的。如果只有一个惯性系,用牛顿理论就可以,没有狭义相对论的事,这个惯性系可以看成是狭相中的一个局域平坦均匀时空。
任何以低于光速的速度运动的粒子的世界线,局部的看,相邻事件之间的距离都是类时的。在这个意义上,我们可以把这种世界线说成是类时的。
如果A和B都以近光速运动,它们之间还是可以用光速相连,这是狭义相对论判断是否存在 “ 因果结构 ” 关系的 “ 光速不变 ” 假设;假如一旦A或B超过光速,A和B之间的关系就是类空的(相邻事件的时空距离是类空的),它们中有一方能观察到另一方的 “ 过去 ” 情况,它们之间不可能有 “ 因果结构 ” 的联系。
狭义相对论的基本出发点是任何粒子都不可能运动得比光更快,光速是一个绝对恒星。这就是说, l秒钟内任何粒子走过的距离不可能大于 3
0公里,而光则精确地走过这个距离。在时空图上是这样来显示的,所有粒子的世界线(用以称呼时空轨迹的名词)都位于光锥内部,而作为极限的光子(光的粒子)世界线则严格地座落在光锥面上,因为光锥正是由光线来规定的。
在明可夫斯基时空里,光速是信号传递的极限速度,这使得其因果结构与牛顿时空的大不相同。对某一事件 E光锥把所有的时空事件分成两种:能够被来自 E的电磁信号所影响的事件(光锥内部)和不可能被影响的事件(光锥外部,或称 “ 外界 ” )。狭义相对论禁止任何一条世界线从光锥内穿到外界,也禁止反向穿越(这并不排除完全处于外界区的世界线。有人假设了一种在外界区以超光速运动的粒子,称为 “ 快于 ” ,但是关于这种粒子的理论有许多棘手的问题,在实验室里也从来没有探测到其存在)。
总之,光线的轨迹使我们能够构造出一个时空连续体的框架。狭义相对论中没有引力,所有的光锥都是相互平行的,因此,明可夫斯基的时空连续体是刚性的,或者说是平直的。伽利略和牛顿的时空分离的观念被统一的时空观念代替了。
虽然相对论不允许我们运动得比光速更快,但它并非阻碍了而是促进了对深层空间的探索。将上面的双生子故事(其中假定瞬时加速)变一下,现在假定飞船有一个恒定的加速度(相对于它的瞬时惯性参考系),其大小等于地球表面上的引力加速度,这对宇航员来说要舒服得多。飞船的速度将迅速增大到接近于光速,而不能达到光速,飞船上的时间将过得比地球上没得多。按照它自己的钟,飞船将用 2. 5年时间飞到最邻近的恒星(比邻星),它与地球相距 4光年;经过大约 45年,飞船就飞出了 40光年;经过 10年就到了银河系中心,而地球上将是过了 15000年;在 25年里(短于宇航员的年龄),飞船将能在整个可观测的宇宙中邀游一周,行程是 300亿光年!但这时的飞船最好不要再返回地球,因为太阳早已将行星都烧成灰烬,自己也早已熄火。
可是,这个异想天开的航行是实现不了的,因为需要有巨大的能量来维持飞船的加速。最好的方法似乎是把飞船自身的物质转化为前进的能量,但即使转换效率为百分之百,飞船在到达银河系中心时所剩的质量已只有出发时的十亿分之一,一座大山缩成了一只老鼠。
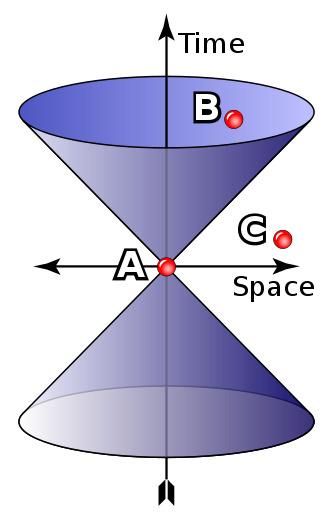
光锥 因为光没有质量,所以它比其他任何事物传播的快----如此快以至于实际上在所有的参考系下它都具有相同的速度。它处于一个特殊的位置,告诉我们有关相对论的时空结构。通过光我们将绘出时空图。为了更好的理解狭义和广义相对论,我们需要理解光锥。
事件--总是占据一定空间和持续一段时间,事件是发生在空间的一点和时间的一瞬的结合。粒子的历史是由一系列事件的排列组成。
当时当地观察者(直接观察)--事件的发生是同时的;其他观察者则需要一定的时间传递过程。
测地线--几何中二点间最简单最短的一条线。
世界线--粒子在每一个时刻占据一个时空点,世界线是这些时空点的集合(积点成线)。
从闵可夫斯基图上的光的轨迹闵可夫斯基时空 中的任一事件,都对应有时空中的一组点的集合能够通过光的轨迹(在闵可夫斯基时空中是直线)与之联系,这组点的集合被称作光锥。在通常的二维空间和一维时间表示中光锥由两个对称的圆锥体组成,它的特性是具有洛伦兹不变性。两个对称的圆锥分别代表了当前事件的过去和未来:
光锥内部的所有点(如左图中的事件B)都可以通过小于光速的速度与当前事件建立因果联系,它们与当前事件的间隔 被称作类时 间隔
s 2 = − t 2
+ x 2 + y 2 + z 2
< 0
光锥表面上的所有点都可以通过光速与当前事件建立因果联系,它们与当前事件的间隔被称作类光 或零性间隔
s 2 = − t 2
+ x 2 + y 2 + z 2
= 0
光锥外部的所有点(如左图中的事件C)都无法与当前事件建立因果联系,它们与当前事件的间隔被称作类空 间隔
s 2 = − t 2
+ x 2 + y 2 + z 2
> 0
由于光锥本身具有洛伦兹不变性,事件之间的间隔属于类时还是类空的也与观察者所在的参考系无关。其中对于类空间隔的事件,由于两者没有因果联系,不能认为它们也具有经典力学 中描述的所谓同时性 ,即无法认为任何类空间隔的两个事件是同时的。
光锥的概念同样可以扩展到广义相对论 中,这时的光锥可以定义为一个事件的因果未来和因果过去的边界,并包含了这个时空中的因果结构 信息。构成光锥的仍然是这个时空中光的世界线 ,此时对应的时空图是彭罗斯-卡特图 。由于在广义相对论中时空可以是弯曲的,光锥也有可能是收缩或倾斜的。
广义相对论 (General Relativity)
等效原理:在处于均匀的恒定引力场影响下的惯性系,所发生的一切物理现象,可以和一个不受引力场影响的,但以恒定加速度运动的非惯性系内的物理现象完全相同。
爱因斯坦提出“等效原理”,即引力和惯性力是等效的。这一原理建立在引力质量与惯性质量的等价性上。根据等效原理,爱因斯坦把狭义相对性原理推广为广义相对性原理,即物理定律的形式在一切参考系都是不变的。物体的运动方程即该参考系中的测地线方程。测地线方程与物体自身固有性质无关,只取决于时空局域几何性质。而引力正是时空局域几何性质的表现。物质质量的存在会造成时空的弯曲,在弯曲的时空中,物体仍然顺着最短距离进行运动(即沿着测地线运动——在欧氏空间中即是直线运动),如地球在太阳造成的弯曲时空中的测地线运动,实际是绕着太阳转,造成引力作用效应。正如在弯曲的地球表面上,如果以直线运动,实际是绕着地球表面的大圆走。
在广义相对论中,引力的作用被“几何化”——即是说:狭义相对论的闵氏空间背景加上万有引力的物理图景在广义相对论中变成了黎曼空间背景下不受力(假设没有电磁等相互作用)的自由运动的物理图景,其动力学方程与自身质量无关而成为测地线方程:
而万有引力定律也代之以爱因斯坦场方程:
<math>R_ - \fracg_ R = - 8 \pi {G \over c^2} T_ </math> 其中
G
为牛顿万有引力常数 该方程是一个以时空为自变量、以度规为因变量的带有椭圆型约束的二阶双曲型偏微分方程。它以复杂而美妙著称,但并不完美,计算时只能得到近似解。最终人们得到了真正球面对称的准确解——史瓦兹解。广义相对论的宇宙现象与科研应用
爱因斯坦方程:
G-ab=T-ab
的思想精髓:物质等于时空的弯曲。
光没有质量,但光有能量,而能量有一个质量(记住一焦耳能量的质量是:M=E/C^2)因此光将有一个向地板弯曲的轨迹,正象外部的观察者所说的那样。
问 (考 )个问题:假设一个人在宇宙中以光速飞行,这时,他手拿一个镜子在脸面前照自己,他能看见镜子中自己的脸吗?
大家都知道中国 “ 矛盾 ” 的典故,也知道外国 “ 万能的上帝是否能造出来一个自己也搬不动的石头 ” 的典故。
这个看似简单的问题,是有点文章的,如果不从假设上做文章,答案只会是:能或不能,但请给点解释。
一直以为人的理解力 (智力 )无上限有下限,今天见到 “ 壮丁 ” 才知道我错了。
怎样判断宇宙的膨胀或收缩呢?这主要是看组成它的百亿星系彼此间的相对运动。那么有没有办法观测宇宙星系彼此运动的情况呢?这些星系是远离我们而去,还是正在向我们靠拢呢?能不能像发现恒星的自行(恒星间在天球上的相对位置的变化)那样,通过比较不同时代拍摄的天文照片来发现星系的自行呢?这至少在目前的技术条件下是不可能的,因为河外星系离我们实在太遥远了。然而,物理学却为我们提供了测定发光物体运动速度的有力手段──多普勒效应,就是通过测定星系发出的光谱线的红移、紫移量来推测它们的运动速度,因为根据多普勒效应,谱线或其频率的相对移动量与相对运动的速度成正比。
用多普勒效应来测定物体的运动速度并不是新鲜事,天文学家在上世纪就已经利用多普勒效应来测算恒星远离我们的速度了。当火车向我们急速开来时,我们会听到它的汽笛声越来越尖锐(音频变高或波长被压缩);反之,当火车远离你而去时,它的汽笛声则变的沉闷(音频变低或波长拉长),这就是物理学上著名的多普勒效应,它是由奥地利物理学家多普勒( 1803 — 1853 )发现的。同声波一样,当光源背离我们运动时,它的光频率变低,可以观测到它的光谱线(例如氢原子谱线)向红端偏移,并且光源离开我们的速度越大谱线的红移量就越大;而光源向我们飞来时,光频变高,光谱线向紫端偏移。这两种情况在天文物理中分别被称作“红移”和“紫移”(紫移也常称为兰移)。我们今天正是用星系光谱的普遍红移,发现了恒星及众多的河外星系远离我们而去──宇宙正在膨胀。
【个人观点】人们常常讨论光速相对速度的问题,许多维相人士不敢正面回答或答非所问,那么,关于光速相对速度的问题,我试试回答如下:
首先用二个相差比较近的速度作假设,如果 A相对于 C以 0.6c的速度向东运动, B相对于 C以 0.6c的速度向西运动。对
于 C来说, A和 B之间的距离以 1.2c的速度增大。这种 “ 速度 ” --两个运动物体之间相对于第三观察者的速度 --可以超过光速 (如果真有可能观察得到的话 )。但是两个物体分别与 C的速度没有超过光速 (0.6c)。两个物体相对于彼此的运动速度也没有超过光速。在这个例子中,根据相对论的观点和计算光速,在 A的坐标系中 B的速度是 0.88c。在 B的坐标系中 A的速度也是 0.88c。并且,它们的时空也有了和第三观察者所在的时空不同。
这也就是相对论的观点。
太阳系行星
《发现》杂志和美国星特朗(Celestron)公司联合主办了“拍宇宙”大赛,本次大赛要求照片必须非常独特,有非常与众不同的视角。但是人们提交的所有作品都没有这张照片更能满足上述要求。这张照片拍摄的是除一颗行星以外的所有太阳系行星,其中甚至包括太阳。
摄影师的构图和这些行星的颜色都恰到好处。红色的火星、绿色天王星和天蓝色海王星。该图还显示了这些行星的相对大小:金星跟地球一样大,但是它处于近地点时,看起来显然比更加遥远的土星更大。更令人不可思议的是,所有这些照片都是在同一天晚上拍摄的。摄影师的创造力,持之以恒的态度和显而易见的激情共同成就了这幅作品。
“
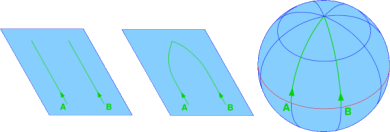
对椭圆轨道的理解符合我们一般的认识,可以想一想如果你朝空中扔一个石块,它在爬升时开始慢下来,在爬升到最高点时速度最慢,然后它冲向地面速度又开始回升。 ”
这种椭圆轨道只能说是因为石块有一个初速度和重力的双重作用,如果石块保持初速度或作匀速运动,就不会有椭圆轨道。而行星都是有某种速度或可以看作匀速运动的。
如果是因为行星之间的相互作用,那么,行星的轨道就会是波动的轨道,因为行星之间的位置在变化,其相互作用力也会变化。
日常生活中,我们用绳子绑一个小石块球作圆周运动,小石块球的轨道就会是圆轨道,想要小石块球作椭圆轨道运动都难。假设太阳和地球之间的引力就象绳子,那么,地球的轨道就应该是圆轨道,至少要会是比较圆吧。
还有一点也不好理解,椭圆轨道是有长轴和短轴之分的,是什么原因使太阳系内的行星都有如此一致的一条长轴方向的椭圆轨道呢?难道 “ 抛石头 ” 的时候都选择了同一个方向来抛出?
一个完整解释 “ 兄弟佯谬 ” 的材料,这是个英文材料,我只看了个大概,感到非常完整,有计算,有图解,有逻辑解释,留这这里大家可以参考。 http://www.relativity.ch/chap15.pdf
一秒被精确定义为铯原子振动 9192631770次 !NISTF-1(在巴黎有个类似的钟是目前世界上最精确的钟 .和世界上另外一些原子能钟一样 .这种可以用来定义宇宙时间坐标 ,进而帮助我们定义光速 ,单位米的长度等等 .但即使是如此精确的钟 ,同样会每 2000万年 "遗漏 "一秒的时间 .所以任何事物都不是完美无缺的!
用科学哲学家的语言说 ,牛顿既是一个唯物主义者 ----他认为物理规律中提到的时间就是时间自身 ----又是一个绝对论者 ----他认为时间独立于任何特定的物理过程之外 .
绝对主义的反对者相对主义坚持认为时间本质上是变化 ,或者是对变化的计量 .关于变化 ,我们说的是在物理物体之间的关系上发生变化 .
以牛顿的观点看来 ,它至少可以假设时间的流逝是没有任何变化的 .但是根据相对主义者的理论 ,这不可能 .时间只是对变化的计量 .没有变化 ,就没有时间 .
在一次著名的争辩中 ,莱布尼茨同样还反驳了牛顿关于时间的观点 ,他说如果牛顿的观点是正确的 ,那么整个世界产生的时间比实际时间早一秒或迟一秒都是有道理的 .莱布尼茨毫不为他未经过验证的假设而担心 .
仅通过伽利略的观察,相同的物理规律约束着无加速度系统,而且其大胆的假设认为光总是以不变的速度传播,这对时间来说是很奇怪的现象。
再次考察一列火车。假设我再车厢正中间提着一盏灯。我打开灯。经车厢里乘客的观察,灯光应该在同一时刻到达火车两端的出口。也就是说,时间 A=灯光到达前门与事件 B=灯光到达后门是同时发生的。
“ 随着火车疾驰而去,你认为它看上去像什么? ”
“ 看上去就好像后门正追赶灯光,而前门正在远离它。 ”
对于路人来说,事件 B要比事件 A早发生。对乘客而言,同时发生的事件在路人看来就不是同时发生的了。
显然,牛顿学说的支持者们不太可能剔除如此激进的观点。他们可能会说光以不同的速度传播,这要根据你所定的参考系。但这已经不是一个选择了,因为我们假定光在任何参考系下传播速度相同。
同时性依赖于谁是观察者,这个想法是爱因斯坦假设中一个具有深刻意义的结果。而且它对时间和空间的本质具有很重要的暗示。
先前,当我们解释牛顿的实践理论和宇宙块时,我们默认了同时性与特定的观察着无关,而只是一个独一无二的全球时间。假如我打响指并且你也打响指,这些事件要么同时发生,要么不是,这与其他人或我们的运动无关。
任何人都在使用相同的独一无二的全球时间来测量时间的流逝。但是在狭义相对论中这不再是一回事了。没有任何人可以遵从独一无二的全球时间。
当我们特地去思考时,就没有时间存在。正如爱因斯坦的老师赫尔姆 • 闵科夫斯基所言,甚至时间都不复存在 ……
“ 自此,空间和事件本身注定将消退为阴影,而且在两者结合中只有一种形式会保留不受他者影响的事实。 ”
“
时间膨胀 ” 的工作原理如下所述。打响你的手指 …… 现在再次打响。把第一次称作事件 A,第二次称作事件 B。通过观察你的手表来计量两次响指的时间间隔为 T,某个运动经过你的人(非加速或减速运动)也通过他们的手表来计量事件 A和 B发生的时间间隔,记为 T^*。
相对论认为 T不必和 T^*相等。诚然 T等于 γ T^*,这里 γ 介于 0和 1之间。
如果超过你的人与你相比运动的很慢,那么 γ 就接近 1,此时 T约等于 T^*。因此你可以认为事件 A和 B得时间间隔在这两种计量方式下是相等的,都为 5秒钟。
但是如果这个人对你来说运动的非常非常快,接近于光速,那么 γ 就近似于 0,此时 T与 T^*差异很大。
对你而言,运动中的钟走慢了。这就是双生子佯谬的原因。
坐在火箭里的那个孪生子的钟要比留在地球上的孪生子的钟走得慢。这就是旅行中的孪生子的 5年对地球上的孪生子而言就有几十年那么长的原因。
美国电视剧《量子跃迁》和《星际跋涉》 看日食 (图片 )
The Michel son-Morley Experiment
In 1887, Albert A. Michelson and Edward W. Morley tried to
measure the speed of the ether . The concept of the ether
was made in analogy with other types of media in which different
types of waves are able to propagate; sound waves can, for example,
propagate in air or other materials. The result of the Michelson-Morley
experiment was that the speed of the Earth through the ether
(or the speed of the ether wind) was zero. Therefore, this
experiment also showed that there is no need for any ether at
all, and it appeared that the speed of light in vacuum was
independent of the speed of the observer! Michelson and Morley
repeated their experiment many times up until 1929, but always with
the same results and conclusions. Michelson won the Nobel Prize in
Physics in 1907.
(The ether was a hypothetical medium in which it was
believed that electromagnetic waves (visible light, infrared
radiation, ultraviolet radiation, radio waves, X-rays,
The Postulates of Special Relativity
On June 30, 1905 Einstein formulated the
two postulates of special relativity:
1. The Principle of Relativity The laws of physics are the same in all inertial frames of
reference.
2. The Constancy of Speed of Light in
Vacuum The speed of light in vacuum has the same value c in all
inertial frames of reference.
The speed of light in vacuum c
(299792458 m/s) is so enormous that we do not notice a delay between
the transmission and reception of electromagnetic waves under normal
circumstances.
The speed of light in vacuum is actually
the only speed that is absolute and the same for all observers as
was stated in the second postulate.
The Postulates of Special Relativity
Inertial Coordinate Systems
From the first postulate, it follows that there is no coordinate
system which is in absolute rest. All motion with constant speed is
relative and any coordinate system moving with constant speed
(relative to the "fixed stars") is called an inertial
coordinate system (or inertial frame [of reference] ).
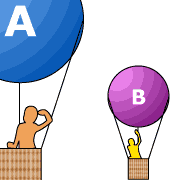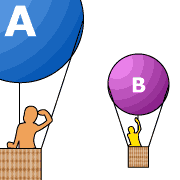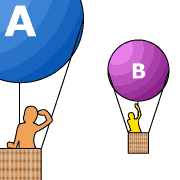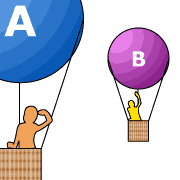
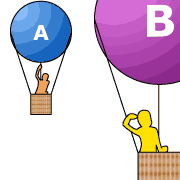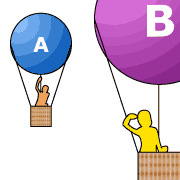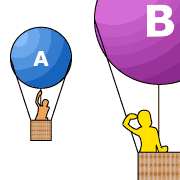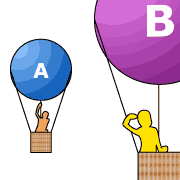
Two inertial frames A and B are moving with
constant speed A will say that objects at rest
in B are moving with respect to A . On the other hand,
an observer at rest in B will say that it is the objects at
rest in A that are moving with respect to B . Motion is
relative!
Actually, Einstein was not influenced so much by
the Michelson-Morley experiment at the time when he wrote down The
Postulates of Special Relativity as he was by his so-called "Gedankenexperimenten"
(imaginary "experiments" in his head) and by Ernst Mach
and his principle, Mach's principle1 , as well as by
Poincaré and his book La Science et l'Hypothèse.
1 Mach's principle: The inertial forces
experienced by a body in nonuniform motion are determined by the
quantity and distribution of matter in the Universe.
The Postulates of Special Relativity
Simultaneity
One of the most important concepts in special relativity is the
one of simultaneity. Two physical events that occur
simultaneously in one inertial frame are only simultaneous in any
other inertial frame if they occur at the same time and at
the same place. Time is relative!
The two figures to the left, seen from two different inertial
frames, help clarify the concept of simultaneity:
Top figure:
Bottom figure:
Lorentz Transformations
A peculiar effect of Einstein's postulates is the transformation
that connects space-time in two inertial frames. Such
transformations are called Lorentz transformations.
The standard Lorentz transformation in the x direction is
(for reference also the classical Galilei transformation is
included):
Lorentz transformation
(special relativity)Galilei transformation
(classical Newtonian mechanics)
where Lorentz
factor . Note that the spatial coordinates (y and z )
perpendicular to the direction of motion (x ) are unchanged.
In the classical limit time
is relative in special relativity.
Directly from Lorentz transformations, one obtains the concepts
of length contraction, time dilation, relativistic Doppler effect,
and relativistic addition of velocities.
Lorentz Transformations
Length Contraction (or Lorentz Contraction)
Suppose that a ruler of rest length v in the direction of its own
length with respect to an observer. The observer, however, will
observe the length to be
This formula is the so-called length contraction formula.
Note that
Lorentz Transformations
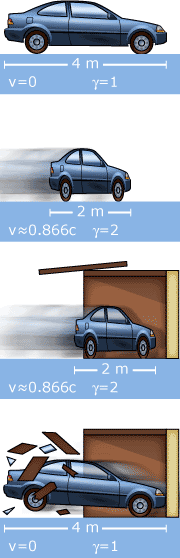
Length Contraction
The length contraction is no "illusion"; it is real in
every way. Consider the "unrealistic" situation of a man
driving a car of rest length 4 m wanting to get it into a 2 m
garage.
He will drive at approximately 0.866 c in order to make
When the car stops in the inertial frame of the garage, it is, in
fact, "rotated in space-time" and will tend to obtain, if
it can, its original length relative to the garage. Thus, if it
survived, it must now either bend or burst the door.
At this moment a "paradox" might occur to the reader:
What about the symmetry of this problem? Relative to the driver,
will not the garage be only 1 m long?
Yes, of course!
How can a 4 m long car get into a 1 m long garage?
Let us consider the situation in the inertial frame of the car.
The open garage now comes towards the car. Because of the concrete
wall, the garage will keep on going even after the crash with the
car, taking the front of the car with it. But the back of the car is
still at rest; it cannot yet "know" that the front has
crashed, because of the finite speed of propagation of information.
Even if the "signal" (in this case the elastic shock wave)
propagates along the car with the speed of light, that signal has 4
m to propagate against the garage front's 3 m, before reaching the
back of the car. This race would be a dead heat if v were
0.75 c , but now v is approximately 0.866 c .
Thus, the car more than just gets into the garage!
Lorentz Transformations
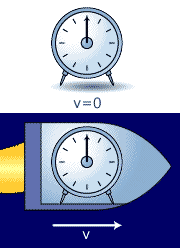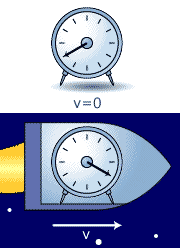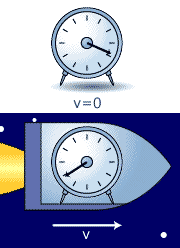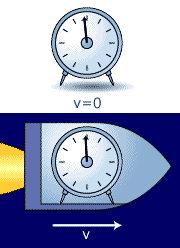
Time Dilation
Moving clocks record their own proper time. (The proper time is
the time recorded by a clock, which moves along with the considered
object.) The proper time interval v relative to an
inertial frame A is given by
where A , i.e.,
Hence time
dilation.
Muons are elementary particles that can be produced when primary
cosmic rays hit the atmosphere of the Earth. The muons are created
at an altitude of around 15 km and the lifetime of the muons (i.e.,
the time which the muons live in their own rest frame) is
approximately 0 = 2.2-6
s. In classical Newtonian mechanics, this would mean that the muons
could in average move approximately c 0
= 660 m before they decay and would not be observed on Earth.
However, a large fraction of the muons do reach the surface of the
Earth.
How can this be explained?
Well, this can be explained in principle in two ways - by either
using length contraction or time dilation. Assume that the muons
move with a speed v close to that of light, e.g., v =
0.999 c .
Time dilation: In the frame of the Earth, the lifetime of the
muons will be 0
v ), which is
approximately 22 0 . This means
that the muons move the distance v
Length contraction: In the rest frame of a muon, the thickness of
the atmosphere is about 10 km/22 = 450 m. But during the lifetime of
the muon, the Earth will move the distance v 0
= 0.999
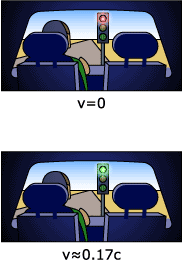
If you are driving towards a red traffic light (c, then the
light from the traffic light will actually appear to be green (c is approximately 5.07
m/s.)
Lorentz Transformations
Relativistic Doppler Effect
The Doppler effect: Motion towards or away from a source will
cause a change in the observed frequency (or wavelength) as compared
to the emitted frequency. All wave phenomena (e.g., water, sound,
and light) behave in this way.
We will discuss below the Doppler effect and the concepts related
to it as well as some formulas when relativistic effects are
considered.
Suppose a source (for example a lamp or even better, a laser)
emits light of frequency c ). Then, an observer moving with a speed v away from the
source, will observe the frequency
This formula is usually called the relativistic Doppler formula.
Note that 0 < v < c, i.e., the frequency which the
observer sees, is smaller than the "original" frequency in
the inertial frame of the source. Thus, the observer moving away
from the source will see a redshift in the frequency of the light,
since light with lower frequencies are "more red" and
light with higher frequencies are "more blue." On the
other hand, an observer moving towards the source will see a
corresponding blueshift. Note that it is only the relative speed
that matters; an observer at rest in an inertial frame looking at a
source moving away from him/her, would also observe a redshift.
当运动沿着波动传递路线 若观察者与波源正以速度频率
其中真空中光速 。
相应的波长 关系式则可写作:
所导致的红移
在非相对论极限下,亦即当
注: 此段落所假设的是观察者和波源互相“远离”。若他们是互相“接近”,则
当运动沿着任意方向 若从观察者参考系 来看,波源以速度
其中
然而,若角度参考系 量测到的(时间点在观察者收到光的时候),则表示式为
在非相对论极限下:
Lorentz Transformations
Relativistic Addition of Velocities
In classical Newtonian mechanics, two different velocities
where
This formula is called the relativistic addition of velocities.
Note that if c
and/or c , then c , and for small velocities c, then the
classical formula is regained.
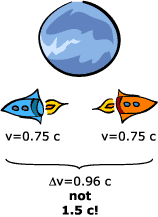
Imagine that you are standing between two space-ships moving away
from you. One space-ship moves to the left with a speed of 0.75 c
(relative to you) and the other one moves to the right also with a
speed of 0.75 c (relative to you).
At what speed will each space-ship see the other moving away?
0.75 c + 0.75 c = 1.5 c? c (according to the
relativistic addition of velocities), and it cannot, of course, be
faster than the speed of light c.
Lorentz Transformations
Space-Time and Minkowski Space
In classical Newtonian mechanics space the three-dimensional
"world" is a place where all the events occur and time is
absolute and the same for everybody. Space and time are separate and
independent of each other and they cannot be mixed in any way.
In special relativity, however, space and time are just different
coordinates of the so-called space-time, i.e., space and time merge
together into a four-dimensional "world". The space
coordinates and the time coordinate are mixed up together by the
so-called Lorentz transformations. Every event corresponds to a
point in space-time. In the words of Minkowski: "Henceforth
space by itself, and time by itself are doomed to fade away into
mere shadows, and only a kind of union of the two will preserve an
independent reality."
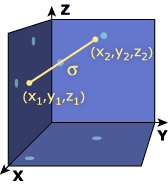
In classical Newtonian mechanics, we measure distances between
two points by the formula
2
= (x1 - x2 )2 + (y1 - y2 )2
+ (z1 - z2 )2 ,
where (x1 , y1 , z1 ) and (x2 ,
y2 , z2 ) are the coordinates of the two points.
This is possible, since we have an absolute concept of simultaneity.
In special relativity, however, the interval between two events is
defined by
s2 = c2 (t1
- t2 )2 - (x1 - x2 )2
- (y1 - y2 )2 - (z1 - z2 )2 ,
where (t1 , x1 , y1 , z1 )
and (t2 , x2 , y2 , z2 ) are
the coordinates of the two events. Note that s2 can in
fact be negative! If we consider two events separated
infinitesimally, (t, x, y, z) and (t + dt, x + dx, y + dy, z + dz),
then the interval becomes
ds2 = c2
dt2 - dx2 - dy2 - dz2 .
This "distance" formula is called the Minkowski metric
and the corresponding four-dimensional "world" is called
the Minkowski space-time or just the Minkowski space
The Twin Paradox
We should state from the very beginning that the twin paradox is
actually no paradox at all. The "paradox" can be clarified
as follows: A pair of twins, Adam and Eve, are thinking of what will
happen to their ages if one of them will go away from Earth on a
space journey. Will Eve for example be younger, older, or have the
same age as her brother if she leaves Earth with a space-ship and
then returns after some time?
Actually, Eve will be younger than her brother when she returns
to Earth. The reason is that Eve is not in the same inertial frame
all the time.
Assume that Adam and Eve are equipped with two watches (one each)
that are synchronized before Eve leaves on her space journey. When
Eve returns to Earth and Adam, the time
However, can you not turn the discussion around and say that Eve
has been at rest in her space-ship while Adam has been on a
"space journey" with planet Earth? In that case, Adam must
be younger than Eve at the reunion!
If these discussions were both correct, then Adam should be both
older and younger than Eve at the same time. But both these
discussions are not correct. Adam is at rest all the time on Earth,
i.e., he is in the same inertial frame all the time, but Eve is not
(as was stated above). Eve will feel forces when her space-ship
accelerates and retards, and Adam will not feel such forces.
P.S. Eve's space-ship has to consume fuel, which
means that it costs to keep yourself young!
Energy is Equivalent to Mass
Energy and mass are related to each other by the well-known
formula E 0 = mc 2 , where E 0
is the rest energy, m is the mass, and c is the speed
of light in vacuum. This means that mass and energy are equivalent.
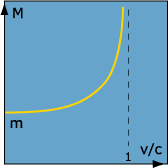
The 'effective' mass M of an object moving relative to an
observer at rest is given by
where E is the energy of the object and m is the
mass of the object. This formula is called the relativistic mass
formula.
Special Relativity as a Tool
At speeds close to the speed of light in vacuum c
relativistic effects become important to consider. Such speeds are
normally not encountered in everyday life. However, special
relativity is used by scientists when doing calculations in, e.g.,
particle kinematics, since the particles often have speeds close to
the speed of light in vacuum. Also in space physics, special
relativity is an important tool.
In 1928, the brilliant English physicist P.A.M. Dirac unified the
quantum theory of W. Heisenberg with special relativity in two
papers named "The Quantum Theory of the Electron." He
received the Nobel Prize in Physics for his contribution as early as
1933. He shared the prize with the Austrian physicist E. Schrödringer,
who played a major role in the development of quantum mechanics. At
a conference dedicated to the one-hundredth anniversary of
Einstein's birth, Dirac said: "Right from the beginning of
quantum mechanics, I was very much concerned with the problem of
fitting it in with relativity. This turned out to be very difficult,
except in the case of a single particle, where it was possible to
make some progress. One could find equations for describing a single
particle in accordance with quantum mechanics, in agreement with the
principle of special relativity. It turned out that this provided an
explanation of the spin of the electron." The equation that
Dirac was talking about is today known as the Dirac equation and
this is the equation describing the dynamics of particles with spin
1/2. Furthermore, Dirac said: " Also, one could develop the
theory a little further and get to the idea of antimatter. The idea
of antimatter really follows directly from Einstein's special theory
of relativity when it is combined with the quantum mechanics of
Heisenberg. There is no escape from it."
History of Special Relativity
Einstein was far from being the only person who contributed to
the development of the theory of special relativity. However, he was
the one who put everything together. Some important years:
1687 Sir Isaac Newton published his book
Philosophiae naturalis principia mathematica (or just Principia ).
In classical Newtonian mechanics, time was universal and absolute.
1873 James Clerk Maxwell completed his
theory of electromagnetism. This theory turned out to be compatible
with special relativity, even though special relativity was not
known at that time.
1887 The famous Michelson-Morley
experiment was performed by Albert Abraham Michelson and Edward
Williams Morley. In the same year, during studies of the Doppler
effect, Woldemar Voigt wrote down what were later to be known as the
Lorentz transformations. The Lorentz transformations were also
written down in 1898 by Joseph Larmor and in 1899 by Hendrik Antoon
Lorentz.
1898 Jules Henri Poincaré said that
"... we have no direct intuition about the equality of two time
intervals."
1904 Poincaré came very close to
special relativity: "... as demanded by the relativity
principle the observer cannot know whether he is at rest or in
absolute motion."
1905 On June 5, Poincaré finished an
article in which he stated that there seems to be a general law of
Nature, that it is impossible to demonstrate absolute motion. On
June 30, Einstein finished his famous article On the
Electrodynamics of Moving Bodies , where he formulated the two
postulates of special relativity. Furthermore, in September,
Einstein published the short article Does the Inertia of a Body
Depend upon Its Energy-Content? In which he derived the formula
E0 =mc2 .
1908 Max Planck wrote an article on
special relativity. He was the second person after Einstein who
wrote an article about this theory. In the same year, Hermann
Minkowski also published an important article about special
relativity.
1915 On November 25, nearly ten years
after the foundation of special relativity, Einstein submitted his
paper The Field Equations of Gravitation for publication,
which gave the correct field equations for the theory of general
relativity (or general relativity for short). Actually,
the German mathematician David Hilbert submitted an article
containing the correct field equations for general relativity five
days before Einstein. Hilbert never claimed priority for this
theory.
重力以及空間中的某一維度或許只是幻覺罷了
大家都看得到,我們周遭的空間具有上下、左右、前後等三個維度。如果把時間加進來,我們就有了一個混合了時間與空間的四維時空。所以,我們就住在一個四維的宇宙裡,不是嗎?
很不可思議的,物理中某些新理論卻預測了三維空間的其中一維可能僅是一種幻覺而已,而構成我們所知世界的一切粒子與場,其實都只是在一個二維的場域中運動罷了,這個二維世界就好似艾波特(A.
Abbott)的名著《平地》(Flatland)所描述的那樣。在這些理論中,重力也是幻覺的一部份:二維世界中並沒有這個力,但是當第三維的幻覺出現時,重力也跟著出現。
講得更精確一點,新理論的預測是空間維度的數目可能會依觀點而異。換句話說,物理學家可以選擇用一組三維空間中的定律(包括重力定律)來描述現實世界,也可以選用另一組二維空間中的定律(不含重力定律)來描述,這兩種描述方式完全等價。儘管這兩種方式截然不同,兩個理論都可以描述我們所看到的一切,以及我們所蒐集關於宇宙如何運行的一切數據。我們根本沒有辦法決定哪一個理論才「真正」算是正確的理論。
上述的這種狀況實在難以想像,還好我們可以在日常生活中找到類似的現象,那就是全像圖。全像圖是二維物體,但是如果我們在適當的光學條件下去看它,就會看到完整的三維圖像。描述三維圖形所需的一切資訊,基本上都記錄在二維的全像圖之中。同樣的,在新理論中,整個宇宙也可能是某種全像圖(見2003年9月號〈資訊.黑洞.全像宇宙〉)。
這種全像式的描述不只是一種智性上或哲學上的有趣東西,它還可能非常有用。譬如說,某個計算在其中一種描述方式下可能非常困難,但在另一種方式中或許就比較單純,因而使得某些令人摸不著頭緒的問題變得比較容易解決。例如最近要分析某項高能物理實驗的結果,這個新理論似乎就有所幫助。除此之外,這種用了全像術概念的理論提供了一種全新的方法,來建構一個量子重力論,亦即遵守量子力學原理的重力論。任何人如果企圖統一所有自然界的力,都會了解量子重力論所扮演的關鍵角色。只有這門學問才能解釋黑洞內到底是什麼樣子,以及大爆炸 後幾奈秒間發生了什麼事情。這些深奧的謎題困擾我們已久,而全像理論提供了可能的解答。
對於鑽研某些研究的物理學家而言,量子重力論是最後的聖杯,因為除了重力之外,其他的物理都可以用量子定律來描述。以量子觀點來描述物理其實代表了物理理論的一整個典範,所以如果只有重力不遵循這個典範,實在是沒有道理的事。量子力學大約出現於80年前,最初是發展來描述原子與次原子世界中各種粒子與力的行為。量子效應只有在這麼小的尺度才會變得重要。在量子理論中,物體沒有明確的位置與速度,而是得用機率與佔據空間某區域的波來描述。在量子世界中,所有的東西在最基本的層次上都會不停的變動,即使是在「真空」中,也有虛粒子不停地出現又消失。
相對的,我們最好的重力理論,即廣義相對論,卻是個古典理論(亦即非量子理論)。廣義相對論是愛因斯坦的傑作,它說物質或能量的聚集會導致時空彎曲,同時這個曲率會讓粒子軌跡轉彎,這正是重力場中粒子該有的行為。廣義相對論是個漂亮的理論,它的很多預測已經通過高度精密的檢驗。
在古典理論中(如廣義相對論),物體具有明確的位置與速度,像是行星繞著太陽運行。我們可以把這些位置與速度(以及物體的質量)代入廣義相對論的方程式中,然後推導出時空的曲率,從而再推導出重力對於物體軌跡的效應。此外,空無一物的時空完全是平滑的──無論我們多仔細地檢驗,這是一個物質與能量能夠四處倘佯不會受到阻礙的場所。
我們如果想建構廣義相對論的量子版本,所要面對的問題並不僅是粒子在原子與電子的尺度上沒有明確的位置與速度而已,更糟的是在普朗克長度(10-33 公分)這種更小的尺度上,量子原理意味著時空本身會是一種洶湧的泡沫,類似於充滿真空中的虛粒子海。當物質與時空這麼變化多端,廣義相對論的方程式能預測出什麼?答案是這些方程式再也不適用。如果我們假設物質遵循量子力學定律,而重力遵循廣義相對論定律,則數學上的矛盾就會出現。無論如何,我們必須找到一個符合量子理論典範的量子重力論。
在多數的情況下,量子力學與廣義相對論的矛盾並不會成為問題,因為通常量子效應與重力效應之一會小到可以忽略,或可以用近似法處理。但是如果時空的曲率很大,重力的量子效應就不可忽視。我們得有非常大的質量或者很高的質量密度,才能產生很大的時空曲率。即使太陽附近所產生的曲率,和讓量子重力效應出現所需的曲率相比,仍是微乎其微。
雖然這些效應目前完全可以忽略,它們在大爆炸 大開始之時曾經非常重要,這就是為什麼我們需要量子重力論來描述大爆炸 如何開始。這樣的理論對於了解黑洞中心所發生的事也很重要,因為那裡的物質擠壓進了時空曲率極高的區域中。既然重力牽涉到時空曲率,量子重力論也將是量子時空理論。這個理論將會澄清到底前面提到的「時空泡沫」是由什麼東西構成的,而且可能會提供我們一個全新的觀點,讓我們了解在自然最深奧的層次上,到底什麼是時空。
弦論是廣被看好的一種建構量子重力論方式,一些理論物理學家自1970年代以來就在研究這項理論。在建構沒有矛盾的量子重力論時,弦論已克服了某些障礙。但我們仍尚未把弦論完全建立起來,也還沒徹底理解它。換句話說,弦論學家只得到了一些弦的近似方程式,而仍不知道精確的方程式。我們也還不知道說明這些方程式形式的基本準則,以及如何從方程式計算出那無數的物理量。
近年來,弦論專家已經獲得很多有趣也令人驚訝的結果,因此我們有了一些新方法來理解量子時空的模樣。我不會在此描述弦論的細節(見2004年10月號〈一統宇宙的弦論〉),而把焦點放在最近弦論中一項非常令人振奮的發展。對於所謂負曲率時空中的重力而言,它導致了一個完整的、邏輯上沒有矛盾的量子描述。這是我們所找到的第一個完整量子描述。我們發現全像理論似乎適用於這些負曲率時空。
負曲率時空
我們都很熟悉歐氏幾何,這種幾何的空間是平的(即不是彎曲的),也就是說它是畫在一張平紙上的圖形。其實就一個極佳的近似而言,這個幾何也是我們周遭這個世界的幾何:平行線永遠不會相交,而且歐幾里得其餘的公設也都成立。
我們也相當熟悉某些彎曲空間。曲率有兩類,正的與負的。最簡單的正曲率空間是球的表面。球有固定的正曲率,也就是說,球上各處的彎曲程度相同(蛋就不一樣了,蛋較尖的端點有較大的曲率)
撰文╱馬多西納 ( Juan Maldacena )
μ介子是一种带负电的基本粒子,质量是电子的207倍。μ介子由宇宙射线与地球大气碰撞形成,每分钟降临每平方米地表的μ介子大约有一万个。
据日本《朝日新闻》网站日前报道,东京大学地震研究所和日本高能加速器研究机构的研究人员开发出一种观测μ介子的量及其飞来方向的装置。这种装置主要是一根5厘米长的塑料棒,被μ介子撞击后,塑料棒会发光。观测装置可以把光转换成电流并记录下来。
实验中,研究人员把新开发的观测装置在一块厚约20厘米的混凝土前后各放置一台,混凝土中有8根钢筋。μ介子穿过钢筋混凝土的时候,碰撞到密度高的钢筋时,前进路线会发生弯曲,不能到达另一侧的观测装置,而未碰撞到钢筋的μ介子可以笔直穿透混凝土,从而被另一侧的观测装置捕捉到。这样,研究人员根据捕捉到的穿过钢筋混凝土墙壁的μ介子的数量,就能判断出墙壁内钢筋的间隔和粗细等。
日本研究人员说,今后可望利用μ介子的这一特性,在不破坏建筑物的前提下,检测建筑物的设计是否科学以及有无偷工减料等。
各位在撰写论文时,特别是在撰写你们人生中第一篇科学论文时,写作步骤建议如下:
初中物理概念汇总 【滑动摩擦、滚动摩擦、静摩擦】
7.牛顿第一定律也称为惯性定律其内容是:一切物体在不受外力作用时,总保持静止或匀速直线运动状态。
十一、电流定律
Bertozzi’s experiment
Figure 8.3
v 2 /c 2
(speed squared in units
of c 2 )
against P/mc 2
(potential energy
in units of mc 2 )
for an electron of mass m
accelerated from zero
initial speed ( c
is speed of light); the
solid line (A) according to classical electrodynamics equation
(6.6), the dashed curve according to relativistic electrodynamics
(equation 6.11) and the dotted
curve (C) according to radiational electrodynamics
(equation 6.23). The solid squares are the result of Bertozzi’s
experiment (Table 6.2).
http://www.musada.net/Papers/Paper8.pdf
1964年,瑞士日内瓦的欧洲联合核子研究中心,高能中性π介子衰变中产生的6KMeV光子,测量80M路线上的飞行时间来确定这里光子的速率,π介子是用19.2KMeV的质子轰击铍靶产生的,他们的速率是0.99975C,这个速率是由同一事件的带电π介子速率推算而来的,利用射束的r-f结构来计时。得出源速相当快、甚至接近光速时发出的光子速率依然是C,实验误差在1.3*10^-4左右。我们现在来考虑一下6KMeV光子的消光距离,根据上述公式可以简单的计算出来,该距离约为5*10^3米。这个实验以非常漂亮的结果无可争辩地证实了,高速运动光源发出光的速率依然是C。
伯托齐(W.Bertozzi)于1964年在麻省理工学院做了一个有名的实验,就是证明电子通过静电加速器(直线加速器)的速度没有超过光速。 http://hi.baidu.com/incinc/blog/item/02263578b6316fe72e73b3b4.html
光是一种人类眼睛可以见的电磁波波长(可见光)。在科学上的定义,光有时候是指所有的电磁波谱。光是由一种称为光子的基本粒子组成。具有粒子性与波动性,或称为波粒二象性。
光没有质量,但光有能量,而能量有一个质量(记住一焦耳能量的质量是: M=E/C^2)因此光将有一个向地板弯曲的轨迹,正象外部的观察者所说的那样。
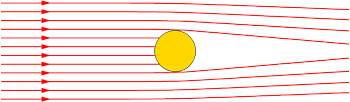
由于能量的质量极小( C^2= 300, 000, 000× 300, 000, 000),这种现象只能在非常强的引力场附近被观察到。这已经被证实:由于太阳的巨大质量,光线在靠近太阳时会发生弯曲。这个试验是爱因斯坦理论(广义相对论)的首次实证。
--------------------------------------------------------
在量子力学的理论中,光子及电子均可视为质点,它在空间中的位置并非局限于一点,而是以机率的方式分布于整个空间。当时间改变后,此一机率分布的方式亦随之改变,其变化的情形有如一种波动,称为机率波。所以严格的说来,质点既非牛顿所说的粒子,也非惠更斯所谈的波动。而光子正是这样的质点,它在传递动量、能量时像个粒子,但不像古典粒子有一定的轨迹;它在遇到狭缝发生绕射时像个波动,但这种波动只代表机率的变化情形。
下面我以双狭缝实验来说明。依照量子力学,一个光子通过双狭缝后,在萤幕上各点出现的机率分布与水波的干涉图案相似。注意,这里说的是出现的机率,如果以侦测器找寻光子的位置,则光子只会在萤幕上的一点出现。 1920年,泰勒( Taylor)使用一微弱光源照射双狭缝。刚开始时,只有少数光子通过双狭缝,它们在萤幕上出现的位置完全是不规律的。然而,萤幕在继续曝光数月之久以后,由于通过的光子数目已多,萤幕上逐渐显出完整的干涉图案来! 1960年代,弗雷格( Pfleeger)和门德耳( Mandel)以雷射光来进行同一实验,得到很漂亮的结果。
当光子数目只有很少几个时,它们的行为像是由机率所控制的粒子;而当一大群光子在一起时,它们的行为就接近马克士威的古典电磁波了。
那么光子与电子的不同处又在那里?第一点,光子是最轻的质点之一,其静止质量为零,电子则带有质量。光子的许多特性莫不归因于此,例如光子最轻,所以速度最快,而带质量的物体其速度均不得超过光速;又例如光束的波动性较电子束显著,乃是由于电子束带有质量,动量较大,而波长较小的缘故。从另一个角度来看,光子轻,能量少。当一光源中的原子加速运动时,只要花费少许能量,即可产生一大群光子。在这群光子束中增加或减少一个光子并不影响其性质,因此光束的粒子性不显著。
光没有质量,但光有能量,而能量有一个质量(记住一焦耳能量的质量是: M=E/C^2)因此光将有一个向地板弯曲的轨迹,正象外部的观察者所说的那样。由于能量的质量极小( C^2= 300, 000, 000× 300, 000, 000),这种现象只能在非常强的引力场附近被观察到。这已经被证实:由于太阳的巨大质量,光线在靠近太阳时会发生弯曲。这个试验是爱因斯坦理论(广义相对论)的首次实证。
其次,光子有物以类聚的特性。这就是当一大群光子在一起时,喜欢聚在相同的运动状态,换言之,光子喜欢以相同的动量、相同的偏极化一起运动,这种性质称为玻色( Bose)统计性。次原子质点如电子、质子等,则与此正相反,它们遵守包立( Pauli )不相容原理,即任何时间皆不准有两个质点拥有相同的动量及自旋。以电子为例来说,在空间中任一轨道上只允许有两个电子,一自旋朝上,一自旋朝下。因此,一群电子在一起时,其运动状态一定是两两不同的,此称为费米( Fermi )统计性。
玻色统计性使光子特别喜欢物以类聚,所以经常是一大群光子在一起,其粒子性自远不如波动性明显。再者,雷射光中之所以能产生极多数相位、波长、偏极化与动量相同的光子,未尝不是拜光子这种群性之赐。由于光子的相位相同,雷射光的相干( coherent)程度很高;由于光子的波长相同,雷射光的颜色很纯,极近单色光;由于光子的偏极化相同,雷射光多具高度的偏极化;又由于光子动量的方向相同,所以雷射光束具有高度的方向性。雷射具有这许多特质,无怪乎能有各方面的应用。
---------------------------------------------------------
根据麦克斯韦的电磁场理论
法拉第证明了变化的磁场可以产生感生电动势 ,麦克斯韦证明了变化的电场可以产生磁场,而感生电动势是可以产生变化的电场的,这样他便将电和磁联系到了一起,创立了电磁学理论。
即空间某处产生了变化电场,在周围空间就要产生变化磁场,这个变化磁场又要在较远的空间产生新的变化电场,接着又要在更远的空间产生新的变化磁场,这样继续下去。这种变化的电场和磁场交替产生、由近及远、以有限的速度在空间内传播的过程,称为电磁波。
这就说明了电磁波是以变化场的形式在空间中传播的,这样就说明了电磁波的传播不需要介质,只要有变化的电场或磁场就行了。
电磁波是变化的电场与变化的磁场相互激发并在空间传播而形成的,它的本质就是场,而这个场也是它自身传播的介质,所以,电磁波是靠其自身来传播的,不需要借助别的介质。
光有波粒二象性,所以通过什么传播说不清
-------------------------------------------------------------
量子理论是科学史上能最精确地被实验检验的理论,是科学史上最成功的理论。量子力学深深地困扰了它的创立者,然而,直到它本质上被表述成通用形式的今天,一些科学界的精英们尽管承认它强大的威力,却仍然对它的基础和基本阐释不满意。
量子世界除了其线度极其微小之外(10-10~10-15m量级),另一个主要特征是它们所涉及的许多宏观世界所对应的物理量往往不能取连续变化的值,(如:坐标、动量、能量、角动量、自旋),甚至取值不确定。许多实验事实表明,量子世界满足的物理规律不再是经典的牛顿力学,而是量子物理学。量子物理学是当今人们研究微观世界的理论,也有人称为研究量子现象的物理学。
量子物理实际上包含两个方面。一个是原子层次的物质理论:量子力学,正是它我们才能理解和操纵物质世界;另一个是量子场论,它在科学中起到一个完全不同的作用。
1900年: 马克斯·普朗克(MaxPlanck)提出量子概念,在他关于热辐射的经典论文中,普朗克假定振动系统的总能量不能连续改变,而是以不连续的能量子形式从一个值跳到另一个值。
通過將物體中的原子看作微小的量子諧振子 ,馬克斯·普朗克 得以獲得了一個黑體輻射的普朗克公式 。但是在引導這個公式時,他不得不假設這些原子諧振子的能量,不是連續的,而是離散的(古典物理學的觀點恰好相反):
E n nh ν
今天這個新的自然常數被稱為普朗克常數來紀念普朗克的貢獻。其值為
h=6.626176*10^-34Js 。
1905年: 阿尔伯特·爱因斯坦(AlbertEinstein)通過擴展普朗克的量子理論,提出不僅僅物質與電磁輻射之間的交互作用是量子化的,而且量子化是一個基本物理特性的理論。他断定:如果振子的能量是量子化的,那么产生光的电磁场的能量也应该是量子化的。尽管麦克斯韦理论以及一个多世纪的权威性实验都表明光具有波动性,爱因斯坦的理论还是蕴含了光的粒子性行为。随后十多年的光电效应实验显示仅当光的能量到达一些离散的量值时才能被吸收,这些能量就像是被一个个粒子携带着一样。
發現通過光照,可以從金屬中打出電子來。同時他們可以測量這些電子的動能。不論入射光的強度,只有當光的頻率,超過一個臨限值後,才會有電子被射出。此後被打出的電子的動能,隨光的頻率線性升高,而光的強度僅決定射出的電子的數量。愛因斯坦提出了光的量子(光子 這個名稱後來才出現)的理論,來解釋這個現象。光的量子的能量為
在光電效應中這個能量被用來將金屬中的電子射出(逸出功 )E w
這裡 m v
1913年: 尼尔斯·玻尔(NielsBohr)提出了一个激进的假设:原子中的电子只能处于包含基态在内的定态上,电子在两个定态之间跃迁而改变它的能量,同时辐射出一定波长的光,光的波长取决于定态之间的能量差。结合已知的定律和这一假设,玻尔扫清了原子稳定性的问题。玻尔的理论充满了矛盾,但是为氢原子光谱提供了定量的描述。
波耳認為電子只能在一定能量E n E n E m
通過吸收同樣頻率的光子,可以從低能的軌道,躍到高能的軌道上。
波耳模型可以解釋氫原子 ,改善的波耳模型,還可以解釋只有一個電子的離子,即
He+ , Li2+ , Be3+
等。但無法準確地解釋其它原子的物理現象。
1919年: 柯林頓·戴維森 等人,首次成功地使用電子進行了繞射 試驗,路易·德布羅意 由此提出粒子擁有波性,其波長與其動量相關
簡單起見這裡不詳細描寫戴維森等人的試驗,而是描寫電子的雙狹縫實驗 。通過這個試驗,可以非常生動地體現出多種不同的量子力學現象。
1923年: 路易·德布罗意(LouisdeBroglie)在他的博士论文中提出光的粒子行为与粒子的波动行为应该是对应存在的。他将粒子的波长和动量联系起来:动量越大,波长越短。
1923年: 尼爾斯·波耳提出了對應原理 ,認為量子數(尤其是粒子數)高到一定的極限後的量子系統,可以很精確地被古典理論描述。這個原理的背景是,事實上,許多巨觀系統,可以非常精確地被古典理論,如古典力學和電磁學來描寫。因此一般認為在非常「大」的系統中,量子力學的特性,會逐漸退化到古典物理的特性,兩者並不相抵觸。因此,對應原理是建立一個有效的量子力學模型的重要輔助工具。量子力學的數學基礎是非常廣泛的,它僅要求狀態空間是希爾伯特空間,其可觀察量是線性的算符。
1924年夏天: 萨地扬德拉·N·玻色(SatyendraN.Bose)提出了一种全新的方法来解释普朗克辐射定律。他把光看作一种无(静)质量的粒子(现称为光子)组成的气体,这种气体不遵循经典的玻耳兹曼统计规律,而遵循一种建立在粒子不可区分的性质(即全同性)上的一种新的统计理论。爱因斯坦立即将玻色的推理应用于实际的有质量的气体从而得到一种描述气体中粒子数关于能量的分布规律,即著名的玻色-爱因斯坦分布。
从1925年元月到1928年元月:
1> 沃尔夫刚·泡利(WolfgangPauli)提出了不相容原理,为周期表奠定了理论基础。( Pauli )不相容原理,即任何时间皆不准有两个质点拥有相同的动量及自旋。以电子为例来说,在空间中任一轨道上只允许有两个电子,一自旋朝上,一自旋朝下。因此,一群电子在一起时,其运动状态一定是两两不同的,此称为费米( Fermi )统计性。
2> 韦纳·海森堡(WernerHeisenberg)、马克斯·玻恩(MaxBorn)和帕斯库尔·约当(PascualJordan)提出了量子力学的第一个版本,矩阵力学。1925年,海森堡基于物理理论只处理可观察量的认识,抛弃了不可观察的轨道概念,并从可观察的辐射频率及其强度出发,和玻恩、约尔丹一起建立起矩阵力学;1926年,薛定谔基于量子性是微观体系波动性的反映这一认识,找到了微观体系的运动方程,从而建立起波动力学,其后不久还证明了波动力学和矩阵力学的数学等价性;狄拉克和约尔丹各自独立地发展了一种普遍的变换理论,给出量子力学简洁、完善的数学表达形式。
3> 埃尔温·薛定谔(ErwinSchrodinger)提出了量子力学的第二种形式,波动力学。在波动力学中,体系的状态用薛定谔方程的解——波函数来描述。矩阵力学和波动力学貌似矛盾,实质上是等价的。量子力学与经典力学的差别首先表现在对粒子的状态和力学量的描述及其变化规律上。在量子力学中,粒子的状态用波函数描述,它是坐标和时间的复函数。为了描写微观粒子状态随时间变化的规律,就需要找出波函数所满足的运动方程。这个方程是薛定谔在1926年首先找到的,被称为薛定谔方程。
4> 费米(Fermi)-狄拉克(Dirac)统计--电子被证明遵循一种新的统计规律,一群电子在一起时,其运动状态一定是两两不同的,此称为费米( Fermi )统计性。 人们进一步认识到所有的粒子要么遵循费米-狄拉克统计,要么遵循玻色-爱因斯坦统计,这两类粒子的基本属性很不相同。
5> 海森堡阐明测不准原理。当微观粒子处于某一状态时,它的力学量(如坐标、动量、角动量、能量等)一般不具有确定的数值,而具有一系列可能值,每个可能值以一定的几率出现。当粒子所处的状态确定时,力学量具有某一可能值的几率也就完全确定。这就是1927年,海森伯得出的测不准关系,同时玻尔提出了并协原理,对量子力学给出了进一步的阐释。
最著名的不相容可觀察量,是一個粒子的位置 x p Δx 和
Δp
的乘積,大於或等於普朗克常數的一半:
這個公式被稱為不確定性原理。它是由海森堡首先提出的。不確定的原因是位置和動量的測量順序,直接影響到其測量值,也就是說其測量順序的交換,直接會影響其測量值。[1]
不過,在今天的理論中,不確定性不是單一粒子的屬性,而是一個系綜 相同的粒子的屬性。這可以視為一個統計 問題。不確定性是整個系綜的不確定性。也就是說,對於整個系綜來說,其總的位置的不確定性
Δx
和總的動量的不確定性 Δp
,不能小於一個特定的值:
6> 保尔·A·M·狄拉克(PaulA.M.Dirac)提出了相对论性的波动方程用来描述电子,解释了电子的自旋并且预测了反物质。
7> 狄拉克提出电磁场的量子描述,建立了量子场论的基础。
8> 玻尔提出互补原理(一个哲学原理),试图解释量子理论中一些明显的矛盾,特别是波粒二象性。
1928年: 量子力学的基础本质上已经建立好了。
量子力学的创建触发了科学的淘金热。早期的成果有:1927年海森堡得到了氦原子薛定谔方程的近似解,建立了原子结构理论的基础;JohnSlater,DouglasRaynerHartree,和VladimirFock随后又提出了原子结构的一般计算技巧;FritzLondon和WalterHeitler解决了氢分子的结构,在此基础上,LinusPauling建立了理论化学;ArnoldSommerfeld和泡利建立了金属电子理论的基础,FelixBloch创立了能带结构理论;海森堡解释了铁磁性的起因。1928年GeorgeGamow解释了α放射性衰变的随机本性之谜,他表明α衰变是由量子力学的隧道效应引起的。随后几年中,HansBethe建立了核物理的基础并解释了恒星的能量来源。随着这些进展,原子物理、分子物理、固体物理和核物理进入了现代物理的时代。
量子体系的古怪性质起因于所谓的纠缠态--量子糾纏 ,简单说来,量子体系(如原子)不仅能处于一系列的定态,也可以处于它们的叠加态。测量处于叠加态原子的某种性质(如能量),一般说来,有时得到这一个值,有时得到另一个值。但是可以构造处于纠缠态的双原子体系,使得两个原子共有相同的性质。当这两个原子分开后,一个原子的信息被另一个共享(或者说是纠缠)。这一行为只有量子力学的语言才能解释。这个效应太不可思议以至于只有少数活跃的理论和实验机构在集中精力研究它,论题并不限于原理的研究,而是纠缠态的用途;纠缠态已经应用于量子信息系统,也成为量子计算机的基础。
1926年: 狄拉克提出量子场论--量子物理的另一个分支。量子力学和狭义相对论的结合产生了相对论量子力学。经狄拉克、海森伯(又称海森堡,下同)和泡利(pauli)等人的工作发展了量子电动力学。20世纪30年代以后形成了描述各种粒子场的量子化理论——量子场论,它构成了描述基本粒子现象的理论基础。激发提出量子场论的问题是电子从激发态跃迁到基态时原子怎样辐射光。1916年,爱因斯坦研究了这一过程,并称其为自发辐射,但他无法计算自发辐射系数。解决这个问题需要发展电磁场(即光)的相对论量子理论。量子力学是解释物质的理论,而量子场论正如其名,是研究场的理论,不仅是电磁场,还有后来发现的其它场。尽管量子场论是困难的,但它的预测精度是所有物理学科中最为精确的,同时,它也为一些重要的理论领域的探索提供了范例。
对称状态的粒子被称为玻色子,反对称状态的粒子被称为费米子。此外自旋的对换也形成对称:自旋为半数的粒子(如电子、质子和中子)是反对称的,因此是费米子;自旋为整数的粒子(如光子)是对称的,因此是玻色子。
这个深奥的粒子的自旋、对称和统计学之间关系,只有通过相对论量子场论才能导出,但它也影响到了非相对论量子力学中的现象。费米子的反对称性的一个结果是包立不相容原理,即两个费米子无法占据同一状态。这个原理拥有极大的实用意义。它表示在我们的由原子组成的物质世界里,电子无法同时占据同一状态,因此在最低状态被占据后,下一个电子必须占据次低的状态,直到所有的状态均被满足为止。这个现象决定了物质的物理和化学特性。
费米子与玻色子的状态的热分布也相差很大:玻色子遵循玻色 -爱因斯坦统计,而费米子则遵循费米 -狄拉克统计。
量子场论的杰出作用体现在它解释了与物质本质相关的一些最深刻的问题。它解释了为什么存在玻色子和费米子这两类基本粒子,它们的性质与内禀自旋有何关系;它能描述粒子(包括光子,电子,正电子即反电子)是怎样产生和湮灭的;它解释了量子力学中神秘的全同性,全同粒子是绝对相同的是因为它们来自于相同的基本场;它不仅解释了电子,还解释了μ子,τ子及其反粒子等轻子。
通過量子場論的發展產生了真正的相對論量子理論。量子場論不但將可觀察量如能量或者動量量子化了,而且將媒介交互作用的場量子化了。第一個完整的量子場論是量子電動力學,它可以完整地描寫電磁交互作用。
強交互作用 的量子場論是量子色動力學 ,這個理論描述原子核所組成的粒子(夸克 和膠子 )之間的交互作用。弱交互作用 與電磁交互作用結合在電弱交互作用 中。
量子力學可以算作是被驗證的最嚴密的物理理論之一了。至今為止,所有的實驗數據均無法推翻量子力學。大多數物理學家認為,它「幾乎」在所有情況下,正確地描寫能量和物質的物理性質。雖然如此,量子力學中,依然存在著概念上的弱點和缺陷,除上述的萬有引力的量子理論的缺乏外,至今為止對量子力學的解釋存在著爭議。
量子力学的基本原理包括量子态的概念,运动方程、理论概念和观测物理量之间的对应规则和物理原理。在量子力学中,一个物理体系的状态由态函数表示,态函数的任意线性叠加仍然代表体系的一种可能状态。状态随时间的变化遵循一个线性微分方程,该方程预言体系的行为,物理量由满足一定条件的、代表某种运算的算符表示;测量处于某一状态的物理体系的某一物理量的操作,对应于代表该量的算符对其态函数的作用;测量的可能取值由该算符的本征方程决定,测量的期待值由一个包含该算符的积分方程计算。
人们对观察结果用经典物理学语言描述时,发现微观体系在不同的条件下,或主要表现为波动图象,或主要表现为粒子行为。而量子态的概念所表达的,则是微观体系与仪器相互作用而产生的表现为波或粒子的可能性。
量子力学表明,微观物理实在既不是波也不是粒子,真正的实在是量子态。真实状态分解为隐态和显态,是由于测量所造成的,在这里只有显态才符合经典物理学实在的含义。微观体系的实在性还表现在它的不可分离性上。量子力学把研究对象及其所处的环境看作一个整体,它不允许把世界看成由彼此分离的、独立的部分组成的。
在量子力学中,不确定性指测量物理量的不确定性,由于在一定条件下,一些力学量只能处在它的本征态上,所表现出来的值是分立的,因此在不同的时间测量,就有可能得到不同的值,就会出现不确定值,也就是说,当你测量它时,可能得到这个值,可能得到那个值,得到的值是不确定的。只有在这个力学量的本征态上测量它,才能得到确切的值。
由於從原則上,無法徹底確定一個量子物理系統的狀態,因此在量子力學中內在特性(比如質量 、電荷 等)完全相同的粒子之間的區分,失去了其意義。在古典力學中,每個粒子的位置和動量,全部是完全可知的,它們的軌跡可以被預言。通過一個測量,可以確定每一個粒子。在量子力學中,每個粒子的位置和動量是由波函數表達,因此,當幾個粒子的波函數互相重疊時,給每個粒子「掛上一個標籤」的做法失去了其意義。
這個全同粒子
(identical particles )
的不可區分性,對狀態的對稱性 ,以及多粒子系統的統計力學 ,有深遠的影響。比如說,一個由全同粒子組成的多粒子系統的狀態,在交換兩個粒子「1」和粒子「2」時,我們可以證明,不是對稱的
玻色子 ,反對稱狀態的粒子被稱為費米子 。此外自旋 的對換也形成對稱:自旋為半數的粒子(如電子、質子 和中子 )是反對稱的,因此是費米子;自旋為整數的粒子(如光子)是對稱的,因此是玻色子。
這個深奧的粒子的自旋、對稱和統計學之間關係,只有通過相對論量子場論 才能導出,但它也影響到了非相對論量子力學中的現象。費米子的反對稱性的一個結果是包立不相容原理 ,即兩個費米子無法佔據同一狀態。這個原理擁有極大的實用意義。它表示在我們的由原子組成的物質世界裡,電子無法同時佔據同一狀態,因此在最低狀態被佔據後,下一個電子必須佔據次低的狀態,直到所有的狀態均被滿足為止。這個現象決定了物質的物理和化學特性。
量子力学处理微观体系的步骤:
1. 根据体系的物理条件,写出它的势能函数,进一步写出 Hamilton算符及 Schrodingger方程。
2. 解Schrodinger方程,根据边界条件求ψn和En。
3. 描绘出ψn、︱ψn︱等的图形,并讨论其分布特点。
4.
由上面求得的,进一步求出各个对应状态的各种力学量的数值,从中了解体系的质。
5. 联系实际问题,对求得的结果加以应用。
对于我们周围的低能世界,量子力学已足够精确,但对于高能世界,相对论效应作用显著,需要更全面的处理办法,量子场论的创立调和了量子力学和狭义相对论的矛盾。
至今為止,僅僅萬有引力 無法使用量子力學來描述。因此,在黑洞 附近,或者將整個宇宙作為整體來看的話,量子力學可能遇到了其適用邊界。目前使用量子力學,或者使用廣義相對論 ,均無法解釋,一個粒子到達黑洞的奇點 時的物理狀況。廣義相對論預言,該粒子會被壓縮到密度無限大;而量子力學則預言,由於粒子的位置無法被確定,因此,它無法達到密度無限大,而可以逃離黑洞。因此
20
世紀最重要的兩個新的物理理論,量子力學和廣義相對論互相矛盾。
尋求解決這個矛盾的答案,是目前理論物理學的一個重要目標(量子重力 )。但是至今為止,找到重力的量子理論的問題,顯然非常困難。雖然,一些亞古典的近似理論有所成就,比如對霍金輻射 的預言,但是至今為止,無法找到一個整體的量子重力的理論。目前,這個方面的研究包括弦理論 等。
或许,超弦理论是唯一被认为可以解释这一谜团的理论,它是量子场论的推广,通过有长度的物体取代诸如电子的点状物体来消除所有的无穷大量。
量子理论允许在一些地方的能量密度为负,只要它可由在其他地方的正的能量密度所补偿,使得总能量保持为正的。量子理论允许负能量密度的一个例子是所谓的卡西米尔效应,甚至我们认为是“空”的空间也充满了虚粒子和虚反粒子对,它们一起出现分离开,再返回一起并且相互湮灭。
现在,假定人们有两片距离很近的平行金属板。金属板对于虚光子起着类似镜子的作用。事实上,在它们之间形成了一个空腔。它有点像风琴管,只对指定的音阶共鸣。这意味着,只有当平板间的距离是虚光子波长(相邻波峰之间的距离)的整数倍时,这些虚光子才会在平板之中的空间出现。如果空腔的宽度是波长的整数倍再加上部分波长,那么在前后反射多次后,一个波的波峰就会和另一个波谷相重合,这样波动就被抵消了。量子力学与相对论有什么矛盾
-------------------------------------------------------------
众所周知,声波主要是通过空气传播的。空气粒子在声源处受到发声体振动时的挤压和推拉,形成疏密相间的纵波向外传播。也就是说,声波是波,但它的波动性是通过空气粒子表现的:波动是粒子的宏观行为,但单独的空气粒子一定也有它的粒子性。据我所知,目前还没有哪位科学家说过“声音也有波粒二象性”的说法。诸位如果有条件的话可以做做实验,相信不会错的。
-----------------------------------------------------------
距今300多年前,
赫赫有名的英国物理学家兼数学家牛顿创立了光学这门学科。当时,
牛顿认为光是由一种弹性小球组成的。这就是所谓的光的微粒说。
当弹子球在行进过程中撞到边框上就会被弹回。光的反弹也是这样,
光的粒子投射到像镜子那样光滑的表面就可以单向反射。
当光从光疏物质(如空气)进入光密物质(如水或玻璃)时,
由于是两种不同的光媒质,它们对光的吸引作用就有差别。
一般来说,光密物质密度较大,它对光的吸引作用强些;
光疏物质密度较小,它对光的吸引作用弱些。这样,
光束由空气进入水或玻璃中时,
就会折向密度较大的水或玻璃的一侧。
提出了完全不同的另一种学说——光的波动说。
他认为光与声音一样,都是一种空气振动过程,
这种振动像水波那样是一波接一波传递的。这就是光的波动说。
两位科学家各持己见,互不相让。
当时牛顿在科学界的威望要比惠更斯高,
所以大多数人附和牛顿的看法,于是微粒说占了上风。
光波是与无线电波、X射线以及γ射线一样的电磁波,
它们之间的区别仅仅是波长不同。无线电波一般以米为单位,
光波则比无线电波要短得多。
虽能比较满意地解释光在传播过程中产生的反射、折射和干涉现象,
但却解释不了光电效应。
以不连接的形式在空中传播。每一份光叫做一个光量子。
光量子既是一种微粒,又是一种电波。
光子说把几百年来争论不休的两种观点,
即光的微粒说和波动说统一了起来。
光子说是最完美的解释。
-----------------------------------------------------------
光在透明物质中才能传播
光是电磁波没错,但光只是电磁波的一部分,是人可见的那一部分,
所以光在透明物质中才能传播
光线传播是发散的,
光源发出的能量到30米的地方是以光源为球心的30米半径的球面
上均匀分布的。
那么在距离r处单位面积所接收的能量是Q/(4πr^2).
30米处单位面积接收的能力肯定是30公里处单位面积接收能量的
一百万(10^6)倍
若是无数个光子那就要考虑光子的分散和被其他物体吸收!
光的波长就是光在单位时间内通过的位移。
T.Alvager,J.M.Baileyetal,F.J.M.Farly,J.Kjellman,and I.Waillin,Phys.Letters 12,260(1964) Arkiv f.Fye. 81,145(1965)
1909年,喀喇氏(C·Caratheeodory)对内能进行了重新定义:“任何一个物体或物体系在平衡态有一个态函数U,叫做它的内能,当这个物体从第一态经过一个绝热过程到第二态后,它的内能的增加等于在过程中外界对它所做的功W。”
http://202.194.155.226/jdwljpkc/dzjc/37.pdf
电子运动速度 (2008-12-24
06:36:55)
http://zhidao.baidu.com/browse/202?lm=2
统观现行高中物理教材,你会发现每部分知识都涉及电子运动速度问题.=((ke2)/(mr1))1/2
,代入数据得v1=2.2×106米/秒,同理可得电子在第二、第三能级上的运动速度v2=1.1×106米/秒;v3=0.73×106米/秒. 从以上数字可知,电子离核越运其速度越小.vm=2.9×105米/秒 .如果用波长更短的光照射铯,电子飞出铯表面的速度还会更大.从而得知,不同的光照射不同的物质,发生光电效应时电子飞出的最大速度也不同.1.08×105米/秒 .0.74毫米/秒. vm=eεmτ/m≈10-4米/秒,振幅约为10- 6米.=6.5×106米/秒 .
时间计量的相对性
http://210.34.16.248/dxwl/course/chap05/5/main1.htm
测量时间的工具称为钟。原则上任何任何周期性的物理过程都可以作为测量时间的钟,日出日落、月亮圆缺、季节更替,这些过程都有一定的周期性,都可以用来计量时间。当然钟有好坏之分,好的钟意味着其物理过程有严格的周期性。下面我们来讨论一个周期性极好的钟--光钟,其结构如图5.4(a) 所示,其中C 为一个能发射和接收光
脉冲并能够对接收信号作出反应的装置,M 是一个平面镜,它们之间的距离为l C 发出一个光脉冲,经M反射返回而被C 接收,C 一旦接收到光脉冲即刻作出某种反应(如其内部驱动装置使指针跳过一格),同时发出第二个光脉冲,经M 反射返回再次被C 接收,使C 又作出反应( 如其指针再跳过一格) ,同时发出第三个光脉冲,如此循环往复。假设将这样的一个钟放在相对于地面以速度u S ¢ 看来,钟是静止的,其周期为
显然,只要C 和M 之间的距离l
那么,同样这个钟,在地面的观察者S 看来,周期是否也等于D t¢
S 看来,由于钟是运动的,钟里面的光脉冲不再沿同一路线来回,其传播路线为如图5.4(b) 所示的折线,但根据光速不变性假设,其传播速度大小仍为c S 测得钟的周期为D t 5.4(b) ,可得D t
由式(5.3)和(5.4)得
式(5.5) 表明,地面的观察者S 看来,钟的周期变长了,即运动的钟变慢了。钟的运行是一种物理过程,运动的钟变慢意味着运动参照系中物理过程的节奏变慢了,或运动参照系中的时间膨胀了。这一结果表明时间的计量与参照系有关,即时间计量是相对的。
现代物理实验已为相对论的时间膨胀提供了有力的证据。实验上观测到以0.9lc 高速飞行的p 介子平均飞行距离是17.135m ,由此可以推算出在实验室参考系中p 介子的平均寿命为
根据式(5.5) 可推出p 介子的固有寿命(即在与p 介子相对静止的参照系中测得的寿命)为
这一结果与实验值(2.603±0.002)×10 - 8 s 极为吻合。
2.
长度计量的相对性
有了钟以后,要测量一个物体长度就简单了。只要测出光从物体的一端传播到另一端所需的时间,则物体长度等于光速c 5.5(a) 所示的“光尺”,其中C 为一个能发射和接收光
脉冲并配有计时器的装置,M 是一个平面镜
,它们之间用一可滑动的连杆连着。为了测量一个物体的长度,向将物体卡在C 和M之 间,启动C 上面的开关,C 发出一个光脉冲,
同时C 里面的计时器开始计时,当光脉冲传播到M 出时被反射而返回,最后被C 接收,C 接收到光脉冲即刻
停止计时。设C 从发出脉冲到接收脉冲的时间D t ¢
显然,式(5.6) 是与尺和待测物体保持相对静止的观察者S ¢ 得到的。如以上测量过程是在相对地面以速度u S 任何看待上述测量过程?在S 看来,光脉冲传播的同时,尺和待测物体也以速度u 5.5(b) 所示的路线传播,传播速度大小为c S 测得脉冲从C 发出到被
长度计量的相对性(放大 )
C 接收所用时间为D t l 5.5(b) 可得D t l
同时在S 看来,C 中的钟以速度v D t D t ¢
根据式(5.6)~(5.4) 可得
式(5.9) 表明,地面的观察者S 测得,物体的长度变长了。这表明长度的计量也与参照系有关,即
长度计量是相对的。
例5.1
父与子: 有一对父子,父亲30 岁,儿子10 岁那年,父亲去作太空旅行,速度为
,(1) 在儿子看来,他50 岁时,其父亲为几岁(设为x (2) 在父亲看来,他x
解:
(1)
在儿子看来,父亲在运动参照系中,其所有物理过程都变慢了。根据
可得
解得
(2)
在父亲看来,儿子在运动参照系中。设父亲年龄为x =34x ¢
岁,则
解得
以上结果清楚地表明了同时的相对性。在儿子看来,他50 岁与父亲34 岁这两个事件是同时的,但在父亲看来,他34 岁不是与儿子50 岁同时,而是与儿子10.4 岁同时。
*他们二人所经历的时间确实是不同的,生物钟也像原子钟一样会受影响。两兄弟的年龄也可以用他们心跳的次数来测量,宇航员回来时确实只有 26岁,而他的同胞兄弟已 60岁。
这个惊人的结果由法国物理学家泡尔 • 郎之万( PaulLangevin)于 1911年作了解释:
在所有连结两个事件(在双生子故事中是飞船从地球出发和回到地球)的世界线中,没有加速度的那一条所耗的时间最长(图 6)。宇航员在其航程中必须加速和减速,这两种情况的效果并不相抵消,他的原时因而总是比他的兄弟短得多(年龄的差别并不仅仅取决于旅行者的加速度,而且还有赖于航行的总持续时间,这里单讲加速度只是为将宇航员时间与地球时间作比较)。虽然看似荒唐,双生子的幻想故事并不意味着爱因斯坦
相对论的任何内在矛盾,而是表明了时间弹性的必然后果。
例5.2
尽快知道有无外星人的“好办法”: 某外星M 离地球2 万光年( 即光从地球传播到该外星需2万年时间) ,某宇航员以速度u 100 年,问:该宇航员是否可能在有生之年抵达外星?若可能,其速度u
解1: 以地面为参照系。在地面上的观察者看来,运动的宇航员的寿命为
宇航员达到外星M所需时间为2´ 10 4 c /u
解得:
解2: 以宇航员为参照系。在宇航员看来,他的寿命为100 年,但地球和外星M 均以速度u M 之间的距离变为
宇航员达到外星M 所需时间为
所以宇航员在有生之年抵达外星的条件为
解得:
按照相对性假设,物理定律在所有的惯性参照系中具有相同的形式。而在不同惯性系内,时空坐标遵守洛伦兹变换关系,所以相对性假设要求物理规律的数学表达式在洛伦兹变换下保持不变。牛顿运动方程对在伽利略变换下保持不变,但在洛伦兹变换下无法保持不是不变。所以必须对经典力学进行改造,使得力学定律洛伦兹变换下能保持不变。
对经典力学改造的方式有两种,一种是保持相关物理量的定义不变,而对力学定律进行改造,另一种是力学定律的形式不变,当对相关物理量进行重新定义。物理学家研究结果决定采用后者。
1.
相对论质量与动量
在相对论中,动量守恒定律仍然是一条基本的物理定律,而且质点的动量仍定义为
所不同的是在牛顿力学中,质量被认为是与物体
运动无关的恒量,而在相对论中,为了满足动量守恒定律在洛伦兹变换下的不变性,物体的质量与其运动速率有关。下面我们以两物体碰撞为例来讨论物体质量与运动速率的关系。
如图5.7,设在参照系S ¢ v ¢ -
v ¢ m ¢ V ¢
以上过程若从参照系S 看,根据洛伦兹速度变换,碰撞前两物体的速度应分别为
v
1=(u+v')/(1+uv'/c^2)
(5.21)
v2=(u-v')/(1-uv'/c^2)
(5.22)
碰撞后两物体的速度均为
V=(u+v')/(1+uv'/c^2)=-u
(5.23)
设参照系S 测得碰撞前两物体的质量分别为m 1 m 2 S 看来,碰撞前后系统的动量也要守恒,即
由此可得
m1/m2=(V-v2)/(v1-V)
(5.24)
将式(5.21 )- (5.23 )代入式(5.24 )可得
m1/m2=(1+uv'/c^2)/(1-uv'/c^2) =(1-v2^2/c^2)^1/2/(1-v1^2/c^2)^1/2
(5.25)
式(5.25 )
表明,物体的质量m
(1-v^2/c^2)^1/2
成反比,记为
其中k v m =m 0 k m 0
m=m0/(1-v^2/c^2)^1/2
(5.26)
式(5.26 )表明,物体的质量与其速度大小有关,速度越大,其质量也越大。由于速度与参照系有关,所以质量也与参照系有关,在相对论中质量也是相对的。
有了质量公式(5.26) ,结合式(5.20) ,可得到相对论动量的表达式
p=mv=m0v/(1-v^2/c^2)^1/2
(5.27)
在任何关于恒星的讨论中,有一个词会反复出现,即引力。它在恒星诞生时就存在, (开氏度是相对于绝对零度来量度的温度,绝对零度是理论上的最低可能温度,等于摄氏一273度,开氏
在反抗引力的持久斗争中,恒星的主要武器是核能。它的核心就是一颗大核弹,在
基本粒子按其在高密度或低温度时集体行
有两条理由使得史瓦西时空见何极为重要。第一,它是对太阳系中引力场的一个很
全新的量子力学理论预言了密度比任何人所敢想象的都高得多的简并状
丹尼斯’萨顿(Dennis Sutton)这样写道:“科学的前沿总是一种由新的真实、
曲面上两点之间的短程线称为测地线。球面上的测地线即是大圆。 相对论
狭义相对论,是只限于讨论惯性系情况的相对论。牛顿时空观认为空间是平直的、各向同性的和各点同性的的三维空间,时间是独立于空间的单独一维(因而也是绝对的)。狭义相对论认为空间和时间并不相互独立,而是一个统一的四维时空整体,并不存在绝对的空间和时间。在狭义相对论中,整个时空仍然是平直的、各向同性的和各点同性的,这是一种对应于“全局惯性系”的理想状况。狭义相对论将真空中光速为常数作为基本假设,结合狭义相对性原理和上述时空的性质可以推出洛仑兹变换。
广义相对论是爱因斯坦(Albert Einstein)在1915年发表的理论。爱因斯坦提出“等效原理”,即引力和惯性力是等效的。这一原理建立在引力质量与惯性质量的等价性上(目前实验证实,在10-12的精确度范围内,仍没有看到引力质量与惯性质量的差别)。根据等效原理,爱因斯坦把狭义相对性原理推广为广义相对性原理,即物理定律的形式在一切参考系都是不变的。物体的运动方程即该参考系中的测地线方程。测地线方程与物体自身故有性质无关,只取决于时空局域几何性质。而引力正是时空局域几何性质的表现。物质质量的存在会造成时空的弯曲,在弯曲的时空中,物体仍然顺着最短距离进行运动(即沿着测地线运动——在欧氏空间中即是直线运动),如地球在太阳造成的弯曲时空中的测地线运动,实际是绕着太阳转,造成引力作用效应。正如在弯曲的地球表面上,如果以直线运动,实际是绕着地球表面的大圆走。
另一广义相对论的预言是,在像地球这样的大质量的物体附近,时间显得流逝得更慢一些。这是因为光能量和它的频率(每秒钟里光振动的次数)有一关系:能量越大,则频率越高。当光从地球的引力场往上走,它失去能量,因而其频率下降(这表明两个波峰之间的时间间隔变大)。从在上面的某个人来看,下面发生的每一件事情都显得需要更长的时间。利用一对安装在一个水塔的顶上和底下的非常准确的钟,这个预言在 1962年被验证到。发现底下的那只更接近地球的钟走得更慢些,这和广义相对论完全一致。地球上的不同高度的钟的速度不同,这在目前具有相当的实用上的重要性,这是因为人们要用卫星发出的信号来作非常精确的导航。如果人们对广义相对论的预言无知,所计算的位置将会错几英哩!
然而在广义相对论中,情况则相当不同。这时,空间和时间变成为动力量:当一个物体运动时,或一个力起作用时,它影响了空间和时间的曲率;反过来,空间 ── 时间的结构影响了物体运动和力作用的方式。空间和时间不仅去影响、而且被发生在宇宙中的每一件事所影响。正如一个人不用空间和时间的概念不能谈宇宙的事件一样,同样在广义相对论中,在宇宙界限之外讲空间和时间是没有意义的。
多普勒效应。我们已经知道,可见光即是电磁场的起伏或波动,其频率(或每秒的振动数)高达 4到 7百万亿次的振动。对不同频率的光,人的眼睛看起来为不同颜色,最低的频率出现在光谱的红端,而最高频率在蓝端。想像在离开我们一个固定的距离处有一光源 ── 例如恒星 ── 以固定的频率发出光波,显然我们接受到的波频率和发出时的频率一样(星系的引力场没有足够强到对它有明显的效应)。现在假定这恒星光源开始向我们运动,当光源发出第二个波峰时,它离开我们更近一些,这样此波峰到达我们处所用的时间比恒星不动时要少。这意味着,这两个波峰到达我们的时间间隔变小了,所以我们接收到的波的每秒振动数(频率)比恒星静止时高。同样,如果光源离我们而去,我们接收到的波频率就变低了。所以对于光来说,这意味着,当恒星离开我们而去时,它们的光谱向红端移动(红移);而当恒星靠近我们而来时,光谱则蓝移。这个称之为多普勒效应的频率和速度的关系是我们日常所熟悉的,例如我们听路上来往小汽车的声音:当它开过来时,它的发动机的音调变高(对应于声波的高频率);当它通过我们身边而离开时,它的音调变低。光波或无线电波的行为与之类似。警察就是利用多普勒效应的原理,以无线电波脉冲从车上反射回来的频率来测量车速。
然而,宇宙的膨胀使得这光被如此厉害地红移,以至于现在只能作为微波辐射被我们所看到。
弗利德曼对于宇宙作了两个非常简单的假定:我们不论往哪个方向看,也不论在任何地方进行观察,宇宙看起来都是一样的。弗利德曼指出,仅仅从这两个观念出发,我们就应该预料宇宙不是静态的。事实上,弗利德曼在 1922年所做的预言,正是几年之后埃得温 • 哈勃所观察到的结果。
第一个假设:假定我们在比星系间距离更大的尺度下来观察,而不管在小尺度下的差异,则宇宙确实在所有的方向看起来是大致一样的。
第二个假设:从任何其他星系上看宇宙,在任何方向上也都一样。我们知道,这正是弗利德曼的第二个假设。我们没有任何科学的证据去相信或反驳这个假设。我们之所以相信它只是基于谦虚:因为如果宇宙只是在我们这儿看起来各向同性,而在宇宙的其他地方并非如此,则是非常奇异的!在弗利德曼模型中,所有的星系都直接相互离开。这种情形很像一个画上好多斑点的气球被逐渐吹胀。当气球膨胀时,任何两个斑点之间的距离加大,但是没有一个斑点可认为是膨胀的中心。并且斑点相离得越远,则它们互相离开得越快。类似地,在弗利德曼的模型中,任何两个星系互相离开的速度和它们之间的距离成正比。所以它预言,星系的红移应与离开我们的距离成正比,这正是哈勃所发现的。
当人们将广义相对论和量子力学的测不准原理结合在一起时,就可能使空间和时间都成为有限的、但却没有任何边缘或边界。
利用多普勒效应,可由测量星系离开我们的速度来确定现在的宇宙膨胀速度。这可以非常精确地实现。然而,因为我们不是直接地测量星系的距离,所以它们的距离知道得不是非常清楚。所有我们知道的是,宇宙在每 10亿年里膨胀 5%至 10%。然而,我们对现在宇宙的平均密度测量得更不准。我们如果将银河系和其他所有能看到的星系的恒星的质量加起来,甚至是按对膨胀率的最低的估值而言,其质量总量比用以阻止膨胀的临界值的 1%还少。
然而,在我们以及其他的星系里应该有大量的 “ 暗物质 ” ,那是我们不能直接看到的,但由于它的引力对星系中恒星轨道的影响,我们知道它必定存在。况且人们发现,大多数星系是成团的。类似地,由其对星系运动的效应,我们能推断出还有更多的暗物质存在于这些成团的星系之间。将所有这些暗物质加在一起,我们仍只能获得必须用以停止膨胀的密度的十分之一。然而,我们不能排除这样的可能性,可能还有我们未能探测到的其他的物质形式几乎均匀地分布于整个宇宙,它仍可以使得宇宙的平均密度达到停止膨胀所必要的临界值。所以,现在的证据暗示,宇宙可能会无限地膨胀。但是,所有我们能真正了解的是,
既然它已经膨胀了 100亿年,即便如果宇宙还要坍缩,则至少要再过这么久才有可能。这不应使我们过度忧虑 ── 到那时候。除非我们到太阳系以外开拓殖民地,人们早由于太阳的熄灭而死亡殆尽!
在 20年代天文学家开始观察其他星系中的恒星光谱时,他们发现了最奇异的现象:它们和我们的银河系一样具有吸收的特征线族,只是所有这些线族都向光谱的红端移动了同样相对的量。为了理解这个含意,我们必须先理解多普勒效应。我们已经知道,可见光即是电磁场的起伏或波动,其频率(或每秒的振动数)高达 4到 7百万亿次的振动。对不同频率的光,人的眼睛看起来为不同颜色,最低的频率出现在光谱的红端,而最高频率在蓝端。想像在离开我们一个固定的距离处有一光源 ── 例如恒星 ── 以固定的频率发出光波,显然我们接受到的波频率和发出时的频率一样(星系的引力场没有足够强到对它有明显的效应)。现在假定这恒星光源开始向我们运动,当光源发出第二个波峰时,它离开我们更近一些,这样此波峰到达我们处所用的时间比恒星不动时要少。这意味着,这两个波峰到达我们的时间间隔变小了,所以我们接收到的波的每秒振动数(频率)比恒星静止时高。同样,如果光源离我们而去,我们接收到的波频率就变低了。所以对于光来说,这意味着,当恒星离开我们而去时,它们的光谱向红端移动(红移);而当恒星靠近我们而来时,光谱则蓝移。这个称之为多普勒效应的频率和速度的关系是我们日常所熟悉的,例如我们听路上来往小汽车的声音:当它开过来时,它的发动机的音调变高(对应于声波的高频率);当它通过我们身边而离开时,它的音调变低。光波或无线电波的行为与之类似。
在光速“眼”里,25年将可观测的宇宙邀游一周。
可以以最简单的和最朴素的一句话来说明相对论原理:在任何二个惯性参考系中,只要有相对运动和对时间间隔进行同一标准的物理计量,就会有相对论理论。狭义相对论的时间间隔标准只是用了光速不变假设而已。
迈克耳逊-莫雷实验---到底说明了什么?
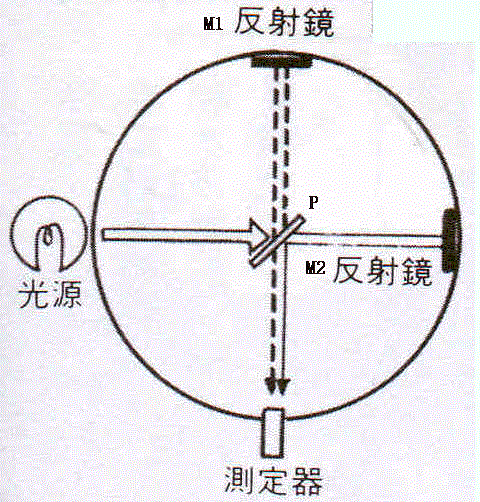
迈克尔逊- 莫雷实验原理
装置如图所示,整个装置可绕垂直于竖直轴转动,P是半镀银镜,M1和M2是两反射镜,互相垂直,PM1=PM2固定不变。从光源S发出的光经P分为两束,再经M1、M2反射后到达目镜T处。这两束光是相干光。假设地球相对于以太沿PM2运行,那么光经PM2来回的时间要长,这两束光在O点相遇时有一定的相位差,因此从T处应该看到这两束光的干涉条纹。
2.里茨在1908年设想光速是依赖于光源的速度的,企图以此解释迈克耳逊-莫雷实验。但是德·希特于1931年在莱顿大学指出,如果是这样的话,那末一对相互环绕运动的星体将会出现表观上的异常运动,而这种现象并没有观察到。由此也证明了爱因斯坦提出的光速和不受光源速度和观察者的影响是正确的,而且既然没有一种静止的以太传播光波振动,牛顿关于光速可以增加的看法就必须抛弃。
有人认为,爱因斯坦在提出狭义相对论的过程中,曾经受到过迈克耳逊-莫雷实验结果的影响。John.Stachel在《爱因斯坦和以太漂移实验》一文中指出,有间接的有力证据表明,爱因斯坦在1889年一定知道迈克耳逊-莫雷实验,并从1889~1901年间,持续感兴趣于设计光学实验,以检查地球穿行于以太的假定运动。
SR Relativistic Transverse
Doppler Effect Recession Wavelength (Approach [-] upper)
牛顿力学
电磁力学
相对论理论
牛顿力学,电磁力学,相对论理论三者本身就是一种三角关系:它们有相互认可的地方,也有相互否认的地方(或通过假设来承认不相容的地方)。这是否表明客观实际本该如此,搞统一理论根本就行不通,要搞也只有增加更多的假设而已。
量子力学和三者根本不同,是单独的一门科学,但量子力学可以引用三者的某些原理。
【前言】V ,则在下面时间,波与观察者会相遇:V ,也即:二个惯性系的前提条件的速度表达式。这就是说:“郭峰君变换”的长度和时间的变换公式没有考虑洛变换因素(3)的一种直接的速度表达式,还没有用到真正的洛变换因素。
闲来无事,在这里帖吧潜水也有好几天了,总感觉有些问题不吐不快。看到很多狭义相对论爱好者所得到的相对论理论,一般都是来自科普书籍。基础理论上的欠缺不少,于是就想在这里开一个系列贴,把大家容易引起误解的问题澄清一下。
从上面的各种情况下的消光定理距离可以看出,不管光离开其光源时速率多大,由于媒质的介入,一个新的扰动来替代他,这个扰动的频率与光原光频率相同,但却以媒质的特征相速度来传播。这时,对媒质的光学性质进行修正以后,相对于媒质静止的观测者测得的光速都将等这种媒质中的光速,使得源的运动和光相对于源的速率无关。这样就使得关于爱因斯坦第二个设定的所有早期实验和许多近代实验的验证全部因为消光定理而失效。
在寻找以太漂移的实验中,最著名的迈克尔逊-莫雷实验(1887)算得上是一个失败的实验,虽然后来的消光定理证实了迈克尔逊-莫雷实验(1887)无实际的物理意义,但是对于寻找以太漂移的实验并未停止,下面我来介绍两个近代著名实验:
我看《光速不变假设》
光速不变假设是狭义相对论和广义相对论的最基本前提,也是反对相对论者和支持相对论者的热点话题之一。本文围绕着这个假设,讨论其支持性论理。
光速不变假设产生的背景
从理解的角度上来看,知道一个人的想法比知道这个人说了什么更重要。这也就是为什么要先了解光速不变假设产生背景的原因。
爱因斯坦在他16岁时的中学时代,就产生了一个 “ 追光 ” 思想实验,即如果他以光速去追赶一束光,会是什么情形呢?后来,爱因斯坦认为这种情形是一个悖论,他描述为:如果他以速度C(真空中的光速)追随一条光线,那么他就应该看到,这样一条光线虽然在空间里振荡,却象一条停滞不前的电磁场。可是,无论是依据经验,还是按照麦克斯韦方程,这样的事情都不可能发生。只要时间或同时性的绝对性这条公理不知不觉地留在人们的潜意识里,那么任何想要令人满意地澄清这个悖论的尝试,都注定要失败。
这是一个逻辑思考,并不牵涉许多其它高深概念。这个悖论并不是想了解真实的光是如何运动的,而是思考:假设光速运动时,既要符合牛顿力学(被认为是与我们的经验事实或感知相近的力学理论),又要符合电磁力学的观点。
牛顿理论认为空间和时间(或同时性)是绝对的, “ 观察 ” 是瞬间的,观察者和被观察者对同一事件的发生都有着一个绝对的同时;任何相同相向速度的运动物体,它们之间的关系就是相对静止的。那么,在绝对时间和空间的条件下,与光速一样速度运动的人就会同时 “ 看到 ” 停滞不前的光;但根据麦克斯韦的电磁场理论,光是一种电磁波,光速是以连续不间断的电磁波形式在电磁场中传递;也就是在任何情况下,电磁场(波)是连续的,而不能是静止的,电磁波一旦产生,就以光速传播,因此不会再有变化。光一旦产生,将以光速运动,而且光速是一个有限速度的恒定值。这就是说,要么光静止,要么光速运动,不能同时存在,牛顿力学和电磁力学在这个悖论上产生矛盾。
从这个逻辑思考中,比较牛顿力学和电磁力学的观点,基于电动力学的精度超牛顿力学几个数量级,有理由认为电磁力学对光速的解释会更加合理些。爱因斯坦基于他描述的悖论的思考,放弃了牛顿力学中时间或同时性的绝对性,选取电磁力学光速传播观点。《电磁学》中的麦克斯韦方程组,能解出 “ 电磁波速在真空中不变,而且数值恒等于光速 c” ,
真空中的光速是一个物理常数(符号是 c),等于 299,792,458米 /秒。这也就是光速不变假设的理论依据。
爱因斯坦 1905年 9月发表在德国《物理学年鉴》上的那篇著名的相对论论文《论动体的电动力学》,提到光速问题的话: “ 光在空虚空间里总是以一确定的速度 V传播着,这速度同发射体的运动状态无关 ” 。一般文章中把这个假设简称为 “ 光速不变 ” --光速与光源运动无关,有些人把这个假设说成光速独立于光源也是十分恰当的。
现在再来看看那个悖论,由于有了光速与光源运动无关的认可以及没有绝对同时性的要求,光一旦发出,任何人都可以看到光了,是 “ 动 ” 光,而不是 “ 静 ” 光了,这样就可以合理解释那个悖论了。
检验光速不变假设的实验
光速不变假设可以合理解释爱因斯坦他所描述的悖论,那又有什么实验支持爱因斯坦的光速不变假设呢?尽管还没有任何实验能证明光速不变这个假设,但一些实验结果却直接或间接地支持这个假设,概括起来,主要有三方面的实验支持。
1)高能中性 π 介子衰变测光速实验
这个实验是最明确的检验相对论光速不变假设的实验。 1964年,瑞士日内瓦的欧洲联合核子研究中心,高能中性 π 介子衰变中产生的 6KMeV光子,测量 80M路线上的飞行时间来确定这里光子的速率, π 介子是用 19.2KMeV的质子轰击铍靶产生的,他们的速率是 0.99975C,这个速率是由同一事件的带电 π 介子速率推算而来的,利用射束的 r-f结构来计时。得出源速相当快、甚至接近光速时发出的光子速率依然是 C,实验误差在 1.3*10^-4左右。我们现在来考虑一下 6KMeV光子的消光距离,根据上述公式可以简单的计算出来,该距离约为 5*10^3米。
这个实验以非常漂亮的结果无可争辩地证实了,高速运动光源发出光的速率依然是 C。
2)迈克耳孙-莫雷实验
在 19 世纪,随着光的波动理论的发展,那时,由于对光的本性知之甚少,人们套用机械波的概念,想像必然有一种能够传播光波的弹性物质,它的名字叫 “ 以太 ” 。为了寻找 “ 以太 ” ,许多科学家进行了大量的工作,最为有名的是迈克耳孙和莫雷所进行的一系列实验。根据理论推导和实验的精度,他们认为如果 “ 以太 ” 存在的话,会有预期的实验现象出现--两束光的干涉条纹移动,实验却得到了否定的结果。
1905年,爱因斯坦抛弃 “ 以太 ” 观念、以光速不变假设和所有惯性系物理规律相同假设的基础上建立了狭义相对论。光在真空的传播不依赖 “ 以太 ” 观念可以更好地解释光速不变的假设。
有些学者认为,根据厄瓦耳 (Ewald1912)和俄辛 (Oseen1915)的消光定理( Extinction
theoremof),从电动力学的角度看来,包括迈克尔逊-莫雷实验 (1887)在内的一些早期光学实验都存在着理论上的缺失。这类实验除了迈克尔逊-莫雷实验 (1887)外,还有双星观测、太阳两个边缘光速和一些其它借用地球以外的光源来做的各类实验。
尽管如此,近代一些更加精确的测试 “ 以太 ” 实验结果还是强有力地否定了 “ 以太 ” ;如1958年的微波激射器实验和1963年的 γ 射线的 “ 无反冲 ” 发射和吸收实验,这两个多普勒频移实验数据表明,可观测到的以太漂移速率与地球轨道速率相比是微不足道的。
3)各类测定光速的实验
光速测定的天文学方法:如:罗默的卫星蚀法(光速测定历史上的第一个记录),布莱德雷的光行差法(恒星的光行差法);
光速测定的大地测量方法:如:伽利略测定光速的方法(物理学发展史上,最早提出测量光速的是意大利物理学家伽利略),旋转齿轮法(不够准确),旋转镜法(不够准确),旋转棱镜法(把齿轮法和旋转镜法结合起来以减少测量误差);
光速测定的实验室方法:如:微波谐振腔法,激光测速法(原理是同时测定激光的波长和频率来确定光速, c=νλ ,精度很高);
随着科技的进步,一方面测定光速的精度在不断提高,另一方面各类测定光速的实验也表明光速近似恒值。根据 1975年第十五届国际计量大会的决议,现代真空中光速的最可靠值是: c=299792.458± 0.001km/s。
任意恒星光行差都长期保持不变,证明:光行差不随时间变化,所以光速也不随时间变化。所有恒星的光行差都为 20.5〃角距,证明:所有恒星的光速都相同。
如何理解光速不变假设
由于光速不变假设的基于解决电磁力学与牛顿力学之间的矛盾,其理论基础是电磁力学,所以,在牛顿力学(经典理论)适用条件下,相对论被人的主观意识认为全是不对的,牛顿的绝对时空观认为距离和时间,在各个参照系测得的都相同,因此光速是相对的,可变的,而不是绝对的,任何速度都是以变化的距离除以所需的时间得到,而且速度是可以叠加的;光速不变假设是不可理解的。对此,再来分析一下经典力学理论(牛顿力学)关于观察或测量运动对象的认识过程。
牛顿力学起源于人们的实际观察或测量经验,实际观察或测量的速度相对于光速来讲,都是比较慢的情形;另一方面,牛顿力学又以公理的形式认为时间和空间都是绝对的(对各个参照系都相同);力的作用时间是瞬间(无限快的);对于观察或测定的运动对象,其观察或测定所需的时间也是默认瞬间的或绝对同时的(或者是用无穷大速度测量)。然而,当用光速运动来思维(因为实际检验做不到)牛顿力学的应用时,就会发现如前面所提到的思维悖论。根本原因就在于:对于观察或测定的运动对象(或研究对象),其观察或测定所需的时间对一个观察者来讲,不能再认为(或默认为)是瞬间的或绝对同时的了,由于运动对象(或研究对象)的速度是如此之快,对观察或测定过程本身所需的时间已经明显表现出来不能再忽略不计。因此,可以从逻辑思考中得出这样的结论:用牛顿力学去计算高速(如接近光速)物体运动会有偏差。
相对论的适用条件,与经典理论不同。相对论不再忽略对观察或测定所需的时间,认为这个时间是客观的并只属于某个观察者(或参照系)的,光速是影响这个时间的一个因素,当参照系发生改变时,那么观察或测定过程所需的时间也就不同了。最重要的一点,是相对论把光速(矢量)引入进来作一种测量的尺度(标量)的考量。光速是人类发现的能传递信息和能量的具普遍意义和具物理意义最快速度,是一种自然而又客观的光速标量尺子。光速不变的假设来源物理意义上的光速,但它己不再是那个实际意义的光速了,在理论上,它已经是一个尺度上的恒量,如同其它任何物理常数一样;尽管这个常数值和实际意义的光速相等,但在概念上是不同的。
一句话,相对论只是用了一个有具体物理意义的光速值作了一个理论意义上的尺度(恒值C)--光速不变假设,已经从具体概念上升为一种抽象概念。在物理学上,相对论这个 “ 光尺 ” (标量)今后所面临的挑战可能只是精度的提高而已。
参考文献:
1.T.Alvager, J.M.Baileyetal, F.J.M.Farly, J.Kjellman, and
I.Waillin, Phys.Letters 12, 260( 1964)
Arkiv f.Fye. 81, 145( 1965)
2.《爱因斯坦奇迹年 ── 改变物理学面貌的五篇论文》 [美 ]
约翰 • 施塔赫尔主编,范岱年、许良英译,上海科技教育出版社 2001年版
第 97─ 98页,第 100─ 101页,第 109页,第 127页。
3.Relativity [美 ]
约翰 • 施塔赫尔主编
4.光速的测量(天文方法)奇迹文库: http://www.qiji.cn/drupal/node/13360
5.光速的测量(地面测量法)奇迹文库: http://www.qiji.cn/drupal/node/13361
6.C.J.Cedarhoim,áG.F.Bland,áB.L.Havens,áandáC.H.Townes,áPhys.Rev.Lettersá1,á342(1958)
7.D.C.Champeney,G.R.Isaak.andáA.M.Khan,áphys.lettersá7,241(1963)
8.《普通物理学 1》大学教材
9.《论动体的电动力学》爱因斯坦
http://www.sciencehuman.com/party/discussion/discusing2006/discusing200607l.htm
http://www.hudong.com/wiki/%E5%85%89%E9%80%9F%E4%B8%8D%E5%8F%98%E5%AE%9A%E5%BE%8B
http://www.google.cn/search?hl=zh-CN&rlz=1T4WZPA_enCA348CA348&q=%E8%B6%85%E5%85%89%E9%80%9F&revid=1596340378&ei=cKMOS_nTGpSDnQfw8PHDAw&sa=X&oi=revisions_inline&resnum=0&ct=broad-revision&cd=6&ved=0CDQQ1QIoBQ
物质在相互作用中作永恒的运动,没有不运动的物质,也没有无物质的运动,由于物质是在相互联系,相互作用中运动的,因此,必须在物质的相互关系中描述运动,而不可能孤立的描述运动。也就是说,运动必须有一个参考物,这个参考物就是参考系。在相对论中,对光速的说法是采用假设法:假定光速不变,在光速不变的前提下,在信息传递速度为光速不变的基础上,爱因斯坦才推出了“相对论”。多少年来,人们真的测出光速不变,光速与光源的运动速度无关,这是为什么呢?只有找到原因,人们才能相信相对论,理解相对论,进一步改造相对论,达到发展物理学的目的。http://www.jibenlizi.cn/new_page_145.htm
推广到普遍的远离情况 理想点以a倍光速远去,1秒钟远离a*C(光速)距离,在计时起位置要a秒传过来,到达a*C的事件将在a 1秒传到观察者,观察者认为速度为a*C/(1 a),速度永远小于光速。a为1时看到以1/2C远离。 当a远小于1时,a*C/(1 a)可近似为a*C,也就是实际速度,当a接近于无穷大时,a*C/(1 a)可近似为C,也就是远离速度远小于测量速度时,测量速度可忽略不记,测量结果约等于真实速度;当远离速度远大于测量速度,测量结果约等于测量速度,也就是测量不到超过测量速度的远离情况。
再来看一下远离的尺 假设有一把尺长1声秒,而我们的测量地面上有一无限长尺子固定不动,运动尺头尾各有一个探测装置,在探测到与地面某一尺刻度重合时,用声音报出该刻度,我们在地面尺原点接收声音。尺匀速运动逐渐远离,当尺尾报0声秒时,尺头已经距离我们1声秒,而这个距离,要1秒后我们才能收到;当尺尾到1声秒距离时,尺头到2声秒,还是要在我们收到尺尾报1声秒后1秒,我们才能收到尺头报2声秒,于是我们会直观的认为,尺尾先到刻度,尺头后到达它本应立刻到达的刻度,感觉好象远离的尺,缩短了。而且运动速度越快,感觉短的越厉害。
看看超过声速会发生什么 超过声速我们将追上钟以前发出的声音,也就是先听到钟敲3下,报3点,再听到钟敲2下,报2点,然后听到钟敲1下,报1点,这就是超过声速时间倒流现象!
普遍的规律是以a倍测量速度靠近的理想点,测量速度显示为a/(1-a)。当运动速度远小于测量速度,测量速度可忽略,测量结果约等于真实速度;当运动速度大于0.5倍测量速度,小于1倍测量速度,将测量到超过测量速度的运动现象;当运动速度等于测量速度,物体将和它的历史信号同时到达,我们将无法区分哪个是历史,哪个是现时,也就无法测量;当运动速度大于测量速度,我们将先收到现时信号,后收到历史信号,会感觉物体在向远方退去,这就是负号的含义,当速度无穷大,近似以测量速度远去。
钟慢、尺缩、超光速时间倒流现象,都可以用声音试验做出结果,这只能证明爱因斯坦的结论有问题,他忽略了测量速度的问题,把现象当成了物理本质。照本文方法解释相对论,双生子悖论、子回出生前杀父悖论都不存在。 而很多号称解释双生子悖论的方法,都是想利用加速度这个问题,将问题推给广义相对论。而我们将双生子放在相同的火箭上在太空中匀速远离,这里没有加速度,相对论应表明运动有相对性,只有时间和长度是绝对的,在任何参照系测量都不变,爱因斯坦扭曲时空的做法,无助于高速运动问题的解决。因此爱因斯坦的相对论需要修正。 爱因斯坦自己的理解,速度无穷大,“绝对同时”有意义,但观测速度上限是光速,因此“绝对同时”无意义。 说明爱因斯坦有时候明白相对论是由于光速太慢,引起的测量问题。如果测量速度无穷大,则同时性的相对性问题不存在。对一群盲人来说,测量速度的上限是声速,则爱因斯坦奉献给他们的伟大理论将是声速相对论,不能因此得出声速最快。”
http://www.hudong.com/wiki/%E7%9B%B8%E5%AF%B9%E8%AE%BA
狭义相对论的时间膨胀效应只有在惯性系中才能给出正确的预言。
http://babyclub.women.sohu.com/r-kpyd-8849-0-0-0.html
1846年,法拉第发现了光的振动面在磁场中发生旋转;1856年,韦伯发现光在真空中的速度等于电流强度的电磁单位与静电单位的比值。他们的发现表明光学现象与磁学、电学现象间有一定的内在关系。1860年前后,麦克斯韦的指出,电场和磁场的改变,不能局限于空间的某一部分,而是以等于电流的电磁单位与静电单位的比值的速度传播着,光就是这样一种电磁现象。这个结论在1888年为赫兹的实验证实。然而,这样的理论还不能说明能产生象光这样高的频率的电振子的性质,也不能解释光的色散现象。到了1896年洛伦兹创立电子论,才解释了发光和物质吸收光的现象,也解释了光在物质中传播的各种特点,包括对色散现象的解释。在洛伦兹的理论中,以太乃是广袤无限的不动的媒质,其唯一特点是,在这种媒质中光振动具有一定的传播速度。
对于像炽热的黑体的辐射中能量按波长分布这样重要的问题,洛伦兹理论还不能给出令人满意的解释。并且,如果认为洛伦兹关于以太的概念是正确的话,则可将不动的以太选作参照系,使人们能区别出绝对运动。1900年,普朗克从物质的分子结构理论中借用不连续性的概念,提出了辐射的量子论。他认为各种频率的电磁波,包括光,只能以各自确定分量的能量从振子射出,这种能量微粒称为量子 ,光的量子称为光子。《物理学年鉴》 发表了爱因斯坦的“关于运动媒质的电动力学”一文。第一次提出了狭义相对论基本原理,文中指出,从伽利略 和牛顿时代以来占统治地位的古典物理学,其应用范围只限于速度远远小于光速的情况,而他的新理论可解释与很大运动速度有关的过程的特征,根本放弃了以太的概念,圆满地解释了运动物体的光学现象。
1905年刚刚得到博士学位的爱因斯坦发表的一篇题为《论动体的电动力学》 的文章引发了二十世纪物理学的另一场革命。文章研究的是物体的运动对光学现象的影响,这是当时经典物理学面对的另一个难题。十九世纪中叶,麦克斯韦建立了电磁场理论,并预言了以光速C传播的电磁波 的存在。到十九世纪末,实验完全证实了麦克斯韦理论。电磁波是什么?它的传播速度C是对谁而言的呢?当时流行的看法是整个宇宙空间充满一种特殊物质叫做“以太”,电磁波是以太振动的传播。但人们发现,这是一个充满矛盾的理论。如果认为地球是在一个静止的以太中运动,那么根据速度叠加原理,在地球上沿不同方向传播的光的速度必定不一样,但是实验否定了这个结论。如果认为以太被地球带着走,又明显与天文学 上的一些观测结果不符。
http://www.hudong.com/wiki/%E3%80%8A%E7%9B%B8%E5%AF%B9%E8%AE%BA%E3%80%8B
爱因斯坦提出了两条基本原理作为讨论运动物体光学现象的基础。第一个叫做相对性原理。它是说:如果坐标系K'相对于坐标系K作匀速运动而没有转动,则相对于这两个坐标系所做的任何物理实验,都不可能区分哪个是坐标系K,哪个是坐标系K′。第二个原理叫光速不变原理 ,它是说光(在真空中)的速度c是恒定的,它不依赖于发光物体的运动速度。http://www.hudong.com/wiki/%E7%9B%B8%E5%AF%B9%E8%AE%BA
洛仑兹(H.A.Lorentz)提出了一个假设,认为一切在以太中运动的物体都要沿运动方向收缩。由此他证明了,即使地球相对以太有运动,迈克尔逊也不可能发现它。爱因斯坦从完全不同的思路研究了这一问题。他指出,只要摒弃牛顿 所确立的绝对空间和绝对时间的概念,一切困难都可以解决,根本不需要什么以太。爱因斯坦提出了两条基本原理作为讨论运动物体光学现象的基础。第一个叫做相对性原理。它是说:如果坐标系K'相对于坐标系K作匀速运动而没有转动,则相对于这两个坐标系所做的任何物理实验,都不可能区分哪个是坐标系K,哪个是坐标系K′。第二个原理叫光速不变原理,它是说光(在真空 中)的速度c是恒定的,它不依赖于发光物体的运动速度。经 典力学 速度的合成法则,对于K′和K这两个做相对匀速运动的坐标系,光速应该不一样。爱因斯坦认为,要承认这两个原理没有抵触,就必须重新分析时间与空间的物理概念。经典力学中的速度合成法则实际依赖于如下两个假设:两个事件发生的时间间隔与测量时间 所用的钟的运动状态没有关系;两点的空间距离与测量距离所用的尺的运动状态无关。爱因斯坦发现,如果承认光速不变原理与相对性原理是相容的,那么这两条假设都必须摒弃。这时,对一个钟是同时发生的事件,对另一个钟不一定是同时的,同时性有了相对性。在两个有相对运动的坐标系中,测量两个特定点之间的距离得到的数值不再相等。距离也有了相对性。数学 条件,即在洛仑兹变换下,带撇的空时变量x'、y'、z'、t'将代替空时变量x、y、z、t,而任何自然定律的表达式仍取与原来完全相同的形式。人们称之为普遍的自然定律对于洛仑兹变换是协变的。这一点在我们探索普遍的自然定 律 方面具有非常重要的作用。
在四维时空里,质量(或能量)实际是四维动量的第四维分量,动量是描述物质运动的量,因此质量与运动状态有关就是理所当然的了。在四维时空里,动量和能量实现了统一,称为能量动量四矢。另外在四维时空里还定义了四维速度,四维加速度,四维力,电磁场方程组的四维形式等。值得一提的是,电磁场方程组的四维形式更加完美,完全统一了电和磁,电场和磁场用一个统一的电磁场张量来描述。四维时空的物理定律比三维定律要完美的多,这说明我们的世界的确是四维的。
------------------------------------------------------------------------------
对光之本性的理论探讨也使人们对光速有所了解。19世纪60年代中期,苏格兰 科学家詹姆斯•克拉克•麦克斯韦创建了一组方程,描述电磁场在空间中的行为。这个方程的一个解表明,电磁波在真空中必须以约为每秒30万公里的速度传播,与罗默及其后人的测量结果相当接近。微波 ,红外线 ,紫外线 ,X射线 和γ射线 ——传播速度的直接测量表明,它们在真空中都有相同的速度。
用于测量光速的实验不断地变得更精确。到20世纪50年代,电子计时装置已经取代了古老的机械设备。20世纪80年代,通过测量激光和频率(f)和波长(λ),运用c=fλ公式计算出了光速(c)。这些计算以米和秒的标准定义为基础,就像现在一样,1米定义为氪-86源产生的光的波长的1,650,763.73倍,1秒则定义为铯-133原子超精细跃迁放出的辐射频率的9,192,631,770倍。这使得c达到非常高的精度,误差只有十亿分之几。
1983年,光速取代了米被选作定义标准,约定为299,792,458米/秒,数值与当时的米定义一致。秒和光速的定义值,表示1米从此定义为光在真空中1/299,792,458秒内走过的距离。因此自1983年以来,不管我们对光速的测量作了多少精确的修正,都不会影响到光速值,却会影响到米的长度。你有多高事实上是由光速定义的。
想象你在一枚火箭里,与一道激光脉冲一同冲入宇宙空间。地球上的观察者会看到这一脉冲以光速远去。无论你相对于地球运动的速度为多少,譬如光速的99%罢,光线仍以光速超越你。看起来似乎很荒谬,但这是真的。使这为真的唯一途径,就是你火箭中的居住者和地球表面的观察者以不同方式衡量时间和空间。
但按照基本力学原理,如果光线偏转,它会被加速。这是否将使光速发生变化,动摇相对论的根本原则?在某种意义上是对的:我们从地球上观察到的光速,在它从太阳附近经过时确实会变化。然而相对论和光速不变原理不能被抛弃。
相对论另一个奇怪的推论是,没有任何物体能加速到光速。不和我们建造动力多么强劲的火箭飞船,它们也永远不能到达光速。这是因为物体运动得越快,其动能越大,惯性也越大。爱因斯坦在他的E=mc2公式中指出,能量和质量或者说惯性相关联。因此一个物体的动能增加,它的惯性也增加,从而越来越难继续加速。这是一个收益递减原理:你对一个物体做的功越多,它就变得越重,加速的效果也越微弱。电子 加速到光速,就需要无限的能量,粒子物理学家们对这一限制深有感触。质子进入美国伊利诺伊州Batawia费米实验室的Tevatron加速器时,它们的速度已经达到光速的99%。加速器的最后阶段使质子的能量提高了100倍,但速度仅增加到光速的99.99995%,与它们进入加速器的速度相比,提高不足1%。量子论 显示一个系统相隔遥远的不同组成部分能够瞬时联系。例如,当一个高能光子衰变成两个低能光子时,它们的状态(例如,是顺时针或逆时针自旋)是不定的,直到对它们中间的某一个作出观察才确定下来。另一个粒子看上去感知到它的同伴被进行了一次观测,结果是任何对第二个粒子的测量总会得到与对第一个粒子的测量相一致的结果。这样远距离的瞬时联系,看起来像是一个讯息以无限大的速度在粒子之间传递了。它被爱因斯坦称为“幽灵式的超距作用”,听起来难以置信,但却是真实的现象。
1993年,加利福尼亚大学伯克利分校的RaymondChiao表明,量子理论还允许另一种超光速旅行存在:量子隧穿。想象朝一堵坚实的墙上踢一个足球,牛顿力学预言它会被弹会,但量子力学预言它还有极小的可能出现在墙的另一面。考虑这种情况的一种途径,是想象它能“借”到足够的能量穿越墙壁,并在到达另一面之后立即将能量归还。这并不违反物理定律,因为最终能量、动量和其它属性都得到了保存。德国物理学家维纳•海森堡的测不准原理表明,在一个系统中,总有某些属性——在这一情况中是能量——的值是不能确定的,因此量子物理学原理允许系统利用这种不确定性,短时间借到一些额外的能量。在隧穿的情况中,粒子从障碍物的一面消失又从另一面重现的需要几乎可以忽略不计,障碍物可以任意的厚——不过随着厚度增加,粒子隧穿的几率也就迅速地朝零的方向递减。
上述这些想法看上去都动摇了禁止超光速的相对论原理。然而它们都没有,因为相对论所禁止的实际上是信息的超光速传输。实验已经表明两个量子物体之间的“瞬时联系”不能用来传递信息。隧穿效应也受到同样的限制。这是由于量子理论是一种内在统计规律,它依赖于大量粒子群体的性质。因此几个光子超越时间是不能用于传递信息的。隧穿效应使输入的波形变形,使之产生一个可能比预期时间更早被接收到的波峰。然而,信息不是由单一波峰携带的,而是由整个波包传送,后者不会运动得比光快。对隧穿效应的谨慎分析结果,似乎支持信号的信息内容仍受到光速限制的说法,尽管这仍是一个有争议的话题。超音速飞机 产生音爆的机理相同。物质介质中运动得比光快的粒子产生的这种辐射称为切伦科夫辐射,常用于检测其它运动得比光快的不可见粒子,例如在东京 宇宙线研究所神岗宇宙粒子研究设施中装满水的巨大探测器里寻找中微子。
-----------------------------------------------------------------------------------
注意,如果麦克斯韦方程正确,而且满足相对性原理,那么可以证明光速不变是正确的,但在爱因斯坦提出狭义相对论的时候还不知道麦克斯韦方程是否正确,于是才把光速不变作为基本假设。
误解来源于语言的不当性。物理学中的很多理解障碍,源于人类提出的问题不恰当、不合理。比如,光的速度是多少?这个问题是不恰当的,因为速度不是一个好的物理量。我们要学会区分物理量的好坏,从而问出有意义的问题
速度为什么不是好的物理量呢?这跟速度的定义有关。速度是定义为空间对时间的导数。这就隐含了一层意思,就是认为时间是标记物体运动的一个参数,空间坐标是时间的函数,所以我们要了解空间关于时间的变化率,也就是速度。
证明光速不变的四项事实。
1) 恒星光行差:任意恒星光行差都长期保持不变,证明:光行差不随时间变化,所以光速也不随时间变化。所有恒星的光行差都为20.5″角距,证明:所有恒星的光速都相同。
2) 恒星都是一个一个的小圆点:恒星都是一个一个的小圆点,证明:任意一个恒星的所有的光线的光速都相同,即没有不同光速的光线。(see
details below)
3) 恒星都静止: 恒星都静止,证明:所有恒星的光速都不随时间变化,都始终恒为常数c不变。这是因为如果光速不断变化,则看起来恒星必然是运动的。证明方法与上述类似,不再重复。
4) 太阳光迈克尔逊——莫雷实验。
因为没有任何光速‘变化’的现象,所以只有采用‘反证法’。
设:某恒星发来两种光速的光线;光速为c的光线,用c表示;光速为C的光线,用C表示;光速c>C
则:t=φ/ω=10×60÷15.0411≈40(秒)
C传播的时间T2=L/C
所以:C=L/T2=946080000c/946080040≈0.9999999577c≈299999.987(公里/秒)
即:如果φ=10′,则c-C=300000-299999.987=0.013(公里/秒)=13(米/秒)
也就是说:如果两条光线的光速差为13米/秒,则这颗距离为30光年的恒星,就同时在角距为10′的A和B两个位置上。
相对论中,时间与空间构成了一个不可分割的整体——四维时空,能量与动量也构成了一个不可分割的整体——四维动量。这说明自然界一些看似毫不相干的量之间可能存在深刻的联系。在今后论及广义相对论时我们还会看到,时空与能量动量四矢之间也存在着深刻的联系。 一 牛顿力学(预备知识 )
二、狭义相对论力学
(注:γ=1/sqr(1-u^2/c^2),β=u/c,u为惯性系速度。)
三、三维证明
1.由实验总结出的公理,无法证明 。洛仑兹变换 :尺缩效应 :钟慢效应 :多普勒效应 是:ν(a)=((u
v1)/(u-v2))ν(b).)
四、四维证明 :无法证明 。
《相对论》是爱因斯坦所著的一部在世界科学理论界影响巨大的著作,主要包括狭义相对论和广义相对论原理的阐述,中文版本由周学政、徐有智编译,编译目录如下:
讨论“同时性的绝对性”
“同时性的绝对性”,其关键词是“时间”。那么要谈“同时性的绝对性”就必须先弄清楚“时间”是什么东西,或者说时间概念的本质定义是什么,然后才能谈得上什么是“同时性的绝对性”。否则讨论就是无本之木而无从谈得上合乎逻辑。
作者:xccchxzw
Dirac的观点倒是干脆,因为实验只能研究出系统坍缩到哪个个态,并且大量实验可以统计出一个概率;但是没法用实验研究出该量子态是如何坍缩的,因此量子态如何坍缩的机制是非物理的问题,按照他的原话,物理学只能描述那些能从实验中研究出来的问题,这种问题属于非实验能研究的问题,故不属于物理学问题。
Dirac还说过:我们以后把量子力学修改成为相对论量子力学的过程将做的工作,不会比当年把Bohr理论修改成为今天的量子力学所做的工作轻松很多。所以不难相信现在的量子理论其实还存在很多的Bug
Hawking认为有3种时间箭头:
科学的学习应当是一学二疑三破。http://tieba.baidu.com/f?kz=671745866
1.1 力学量的‘可观测性’与其算符本征函数族的‘完备性’
===============================================================================================
诺维柯夫自洽性原则 是由俄罗斯 理论物理学家诺维科夫 在1980年代提出的有关时间悖论 的规则。此原则指出,人可以回到过去,但是不能因此改变历史的进程。其基本含义為,我們的世界是已經被改變過的最終結局。
时间悖论 最早是在科幻小说 中提到的。这个悖论的必要前提是:人类可以随心所欲的控制三维空间之后的“第四维”——时间,能够回到过去或者将来。
就严肃的物理学理论而言,爱因斯坦的《相对论》指出,的确存在不违背已知的物理法则改变时间的可能性。
相对论逻辑自洽性探疑
广义相对论认为引力可导致重力红移,即:射入重力势阱中的光会发生蓝移,而相反从势阱中射出的光会发生红移;归纳而言这两种现象被称作重力红移。重力红移已经在实验室中及在天文观测中得到证实和测量,光波从一个大质量物体表面射出时,往引力弱的方向会有频率红移。
另一方面,狭义相对论人为速度也可以导致速度红移,即:远离光源方向的光波会有频率红移。
多普勒效应是当运动在波源后面时,会产生相反的效应。波长变得较长,频率变得较低
(红移 red shift)。
具有波动性的光也会出现这种效应,它又被称为多普勒 -斐索效应 .
因为法国物理学家斐索( 1819~1896年)于 1848年独立地对来自恒星的波长偏移做了解释,指出了利用这种效应测量恒星相对速度的办法 .光波与声波的不同之处在于,光波频率的变化使人感觉到是颜色的变化 .
如果恒星远离我们而去,则光的谱线就向红光方向移动,称为红移;如果恒星朝向我们运动,光的谱线就向紫光方向移动,称为蓝移。
光(电磁波)的多普勒效应计算公式分为以下三种:
The Question
(Submitted March 27, 1998)
I would like to know if it is true, that the theory of relativity
has been proven by some scientists, who made satellite experiments?
What was there discovery and how did they prove it?
The Answer
This topic is fairly broad, so let me try to narrow it a little.
"Relativity" is a rather general term that encompasses
both special and general
relativity . The former encompasses effects such as the changes
in physical properties of objects with speeds approaching that of
light, whereas the latter includes effects having to do with the
bending of "spacetime" by massive
bodies. There is no one experiment which "proves"
relativity, and yet so many experiments have provided consistency
with the "theories", that most scientists accept them as
being extremely accurate in their descriptions of reality.
"Special Relativity": The strongest direct evidence
comes probably from particle accelerators, in which subatomic
particles such as electrons
and positrons
are accelerated to within a few inches per second of the speed
of light . We can observe very clearly and accurately the changes
in, for instance, the apparent masses of the particles. They are
observed to increase dramatically, and in fact new and much heavier
particles can be created by making counter-rotating beams of, say,
electrons and positrons, collide head-on with each other. Special
relativity has played a key role in the design and operation of
particle accelerators for many decades.
"General Relativity": There have been a variety of
experiments over the years which have supported general relativity
in ever more detail. I would say the culmination was the awarding of
the 1993 Nobel Prize in Physics to Russell Hulse and Joe Taylor for
the discovery of the binary pulsar 1913+16. This binary
star system consists of two neutron
stars which are orbiting
about their common center of mass about every 7.75 hrs. Over time,
they are spiraling in toward each other, due to loss of energy via
"gravitational
radiation" - a prediction of general relativity. Other general
relativistic effects are observed, such as the "precession of
the periastron". That is to say, the stars
are in elliptical orbits, and the "long direction" of each
ellipse
is precessing with respect to a distant observer. This effect is
about 4 degrees per year. (In comparison, for Mercury going around
the Sun, it is about 44 seconds of arc per century.)
There are a host of other experiments which confirm different
aspects of both special and general relativity. I view those just
mentioned as among the strongest examples.
J.K. Cannizzo
相对论是否被实验证明了?--美国主流科学家的答复
有人问美国航天物理学家:相对论是否被实验证明了?
英文翻译大致答复如下:
没有任何实验证明了相对论,然而,许多实验与相对论理论一致。基于相对论所描述的精确性,大多数科学家接受它们。( There
is no one experiment which "proves" relativity, and yet so
many experiments have provided consistency with the
"theories", that most scientists accept them as being
extremely accurate in their descriptions of reality. )
对狭义相对论而言,最强最直接的实验证据可能是来自粒子加速器,通过加速电子和质子接近至光速,能清楚和准确地观察到粒子惯性质量( the
apparent masses )的变化。如通过反旋转的质子束和电子束相互对撞( by
making counter-rotating beams of, say, electrons and positrons,
collide head-on with each other),能观察到粒子质量非常明显地增加,实际上,是新的更重的粒子产生了。狭义相对论在粒子加速器的设计和操作上起着关键性的作用。
对广义相对论而言,最了不起的是1993年诺贝尔物理学奖获得者--美国的赫尔斯和泰勒( Russell
Hulse and Joe Taylor )。1974年,他们发现了第一颗射电脉冲双星 PSR1913+ 16( binary
pulsar 1913+16),它们是两颗互相环绕的脉冲星,轨道周期很短,仅为 7.75小时。轨道的偏心率为 0.617。当两颗子星相互靠得很近时,极强的引力辐射会导致它们的距离愈加靠近,轨道周期会逐渐变短。通过精确地测量射电脉冲双星轨道周期的变化可以检测引力波的存在,验证广义相对论。赫尔斯和泰勒也因此获得 1993年的诺贝尔物理学奖。其它方面的三个证据是:日全食时星光在太阳引力场中会发生弯曲;白矮星光谱线波长的红移和水星轨道近日点的反常进动。对水星轨道近日点的反常进动,按照广义相对论,在太阳系中,行星的轨道存在反常进动是普遍现象,离太阳越近的行星反常进动就越明显。水星是距离太阳最近的一颗大行星,利用广义相对论算出的它的反常进动应为每百年 43. 03角秒,这与每百年 43.1角秒的观测值符合得较好。对于金星、地球和卡洛伊斯 (一颗小行星 ),用广义相对论算出的结果与观测值相比较,也在误差允许的范围之内。由此可见,在太阳系内离太阳较近的空间,要精确地计算行星的位置已不能依靠牛顿的万有引力定律,而要用广义相对论了。进动的解释是以上三个证据中最有说服力的。
相对论是否被实验证明了?--美国主流科学家的答复







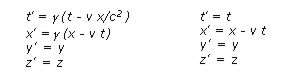





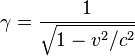
















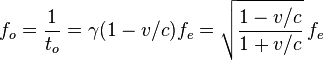 ..........(4)
..........(4)